题目内容
 如图,折线A-B-C-D的每一条线段都平行于矩形的边,它把矩形分成面积相等的两部分.点E在矩形的边上,使得线段AE也平分矩形的面积.已知线段AB=30,BC=24,CD=10,求DE的长.
如图,折线A-B-C-D的每一条线段都平行于矩形的边,它把矩形分成面积相等的两部分.点E在矩形的边上,使得线段AE也平分矩形的面积.已知线段AB=30,BC=24,CD=10,求DE的长.分析: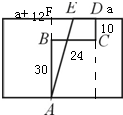
如上图所示,假设D到矩形右宽边的长度为a,延长AB与矩形上边的交点F,假设F到左宽边的距离是a+b,则由折线A-B-C-D的每一条线段都平行于矩形的边,它把矩形分成面积相等的两部分,左右两边的面积相等,即:
(a+b)×(30+10)+24×10=30×24+(10+30)×a,变形,得:40b=(30-10)×24,b=480÷40=12;
这样整个矩形的面积是(30+10)×(a+12+24+a)=40×(2a+36),再根据点E在矩形的边上,使得线段AE也平分矩形的面积,则AE左边的面积等于整个矩形的面积的一半,即左边小矩形面积加三角形AEF的面积等于大矩形面积的一半,列出等式,求出EF的长,则DE就等于24减去EF的长,即可得解.

如上图所示,假设D到矩形右宽边的长度为a,延长AB与矩形上边的交点F,假设F到左宽边的距离是a+b,则由折线A-B-C-D的每一条线段都平行于矩形的边,它把矩形分成面积相等的两部分,左右两边的面积相等,即:
(a+b)×(30+10)+24×10=30×24+(10+30)×a,变形,得:40b=(30-10)×24,b=480÷40=12;
这样整个矩形的面积是(30+10)×(a+12+24+a)=40×(2a+36),再根据点E在矩形的边上,使得线段AE也平分矩形的面积,则AE左边的面积等于整个矩形的面积的一半,即左边小矩形面积加三角形AEF的面积等于大矩形面积的一半,列出等式,求出EF的长,则DE就等于24减去EF的长,即可得解.
解答:解:接以上分析,假设EF=x,则:(a+12)×(30+10)+
×(30+10)x=40×(2a+36)÷2,
40a+480+20x=40a+720,
20x=720-480,
x=240÷20=12,
所以DE=24-12=12;
答:DE的长是12.
| 1 |
| 2 |
40a+480+20x=40a+720,
20x=720-480,
x=240÷20=12,
所以DE=24-12=12;
答:DE的长是12.
点评:假设出a,求出另一侧是a+12是此题的突破口.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
 (2012?浙江)已知:A、B两地之间的距离为900km,C地介于A、B两地之间,甲车从A地驶往C地,乙车从B地经C地驶往A地,已知两车同时在出发,相向而行,结果两车同时到达C地后,甲车因故在C地须停留一段时间,然后返回A地,乙车继续驶往A地,设乙车行驶时间x(h),两车之间的距离为y(km),如图的折线表示y与x之间的关系.
(2012?浙江)已知:A、B两地之间的距离为900km,C地介于A、B两地之间,甲车从A地驶往C地,乙车从B地经C地驶往A地,已知两车同时在出发,相向而行,结果两车同时到达C地后,甲车因故在C地须停留一段时间,然后返回A地,乙车继续驶往A地,设乙车行驶时间x(h),两车之间的距离为y(km),如图的折线表示y与x之间的关系.




