Question

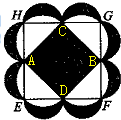如图，阴影正方形的顶点分别是大正方形EFGH各边的中点，分别以大正方形各边的一半为直径向外作半圆，再分别以阴影正方形的各边为直径向外作半圆，形成8个“月牙形”．这8个“月牙形”的总面积为5平方厘米，问大正方形EFGH的面积是多少平方厘米？

Answer 1

分析：如图所示，连接AB和CD相交于O，容易由勾股定理和半圆面积公式得到三角形ACH的面积，即得到三角形AOC的面积等于AH，HC上两个“月牙形”的面积之和．因此，这8个“月牙形”的总面积等于正方形ACBD的面积．由于这8个“月牙形”的总面积为5平方厘米，而正方形EFGH的面积为正方形ACBD的面积的2倍，所以正方形EFGH的面积等于10平方厘米．

解答：解：如图所示，连接AB和CD相交于O，容易由勾股定理和半圆面积公式得到三角形ACH的面积，
即得到三角形AOC的面积等于AH，HC上两个“月牙形”的面积之和；
因此，这8个“月牙形”的总面积等于正方形ACBD的面积；
由于这8个“月牙形”的总面积为5平方厘米，而正方形EFGH的面积为正方形ACBD的面积的2倍，
所以正方形EFGH的面积等于5×2=10平方厘米．

点评：推论得出：8个“月牙形”的总面积等于正方形ACBD的面积，是解答本题的关键．