Question

看看如图那些图形可以密铺，在下面打“√”．

Answer 1

分析：几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．360°为正多边形一个内角的整数倍才能单独镶嵌，即密铺．

解答：解：长方形的每个角都是90°，能除360°，能密铺；
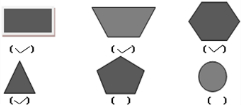
两个完全相同的梯形能组成一个平行四边形，平行四边形能密铺，所以完全相同的梯形也能密铺；
因正六边形的每个内角是120°，能整除360°，能密铺；
因正三角形的每个内角是60°，能整除360°，能密铺；
正五边形的每个角都108°，不能整数360°，不能密铺；
因圆的边线是曲线，不能组成角，所以不能密铺；
故答案为：

点评：本题考查平面密铺的知识，注意掌握只用一种正多边形镶嵌，只有正三角形，正四边形，正六边形三种正多边形能镶嵌成一个平面图案．