Question

用同一种颜色对4×4方格的7个格子进行涂色，如果某列有涂色的方格则必须从最底下的格子逐格往上涂色，相邻两列中左侧的涂色的方格数大于或等于右侧涂色的方格数（如图）．那么共有

9

种涂色的图案．

Answer 1

分析：按照要求把4x4方格的7个格子进行涂色，左侧的涂色的方格数大于或等于右侧涂色的方格数，把7分成几个数的和，左边的数最大是4，例如4+3=7，涂在第一列开始到第三列开始有3种图案；
3+2+2=7，分别从1、2列开始涂色，有2种图案；
3+2+1+1，只有从第1列开始涂色，有1种图案；
4+1+1+1，只有从第1列开始涂色1种图案；
4+2+1=7，分别从1、2列开始涂色，有2种图案；
把它们加起来，即可得解．

解答：解：如图，

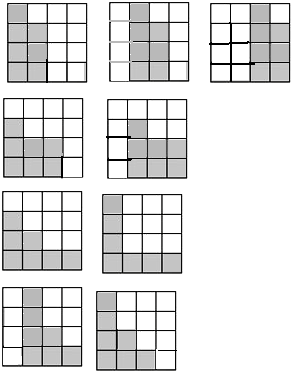
3+2+1+1+2=9（种），
答：那么共有9种涂色的图案．
故答案为：9．

点评：正确理解题意，把7分成几个数的和，然后涂色是解决此题的关键．