题目内容
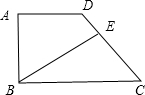 如果所示的直角梯形ABCD中,AD=3厘米,AB=4厘米,BC=6厘米,BE将梯形分成面积相等的两部分,DE:EC=
如果所示的直角梯形ABCD中,AD=3厘米,AB=4厘米,BC=6厘米,BE将梯形分成面积相等的两部分,DE:EC=1
1
:3
3
.分析:连接BD,△ABD是直角三角形,面积=
AB?AD,直角梯形ABCD的面积=
(AD+BC)?AB,因为“BE将梯形分成面积相等的两部分”,所以△BCE的面积=
直角梯形ABCD的面积,△BED的面积=
直角梯形ABCD的面积-△ABD的面积,因为△BCE和△BED等高,所以底边DE:EC=△BED的面积:△BCE的面积,带入数据,即可得解.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:

直角梯形ABCD的面积=
(AD+BC)?AB,
=(3+6)×4÷2,
=18(平方厘米);
△ABD的面积=
AB?AD=3×4÷2=6(平方厘米),
因为△BCE和△BED等高,
所以底边DE:EC=△BED的面积:△BCE的面积,
=(18÷2-6):(18÷2),
=3:9,
=1:3;
答:DE:EC=1:3;
故答案为:1,3.

直角梯形ABCD的面积=
| 1 |
| 2 |
=(3+6)×4÷2,
=18(平方厘米);
△ABD的面积=
| 1 |
| 2 |
因为△BCE和△BED等高,
所以底边DE:EC=△BED的面积:△BCE的面积,
=(18÷2-6):(18÷2),
=3:9,
=1:3;
答:DE:EC=1:3;
故答案为:1,3.
点评:此题考查了两个三角形等底等高时,面积相等;高一定时,三角形的面积与底成正比的关系的灵活应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
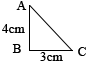 (2008?高邮市)把如图所示的直角三角形ABC以BC为轴旋转一周,可以形成一个
(2008?高邮市)把如图所示的直角三角形ABC以BC为轴旋转一周,可以形成一个
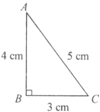 把如图所示的直角三角形ABC沿着AB轴旋转一周,形成
把如图所示的直角三角形ABC沿着AB轴旋转一周,形成 如果所示的直角梯形ABCD中,AD=3厘米,AB=4厘米,BC=6厘米,BE将梯形分成面积相等的两部分,DE:EC=________:________.
如果所示的直角梯形ABCD中,AD=3厘米,AB=4厘米,BC=6厘米,BE将梯形分成面积相等的两部分,DE:EC=________:________.