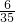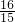题目内容
求最下列每组数的最大公约数与最小公倍数.
24和36;
18、24和40(只求最小公倍数).
解:(1)24和36;
24=2×2×2×3;
36=2×2×3×3;
它们的最大公约数是:2×2×3=12;
最小公倍数是:2×2×3×2×3=72;
(2)18、24和40;
24=2×2×2×3;
18=2×3×3;
40=2×2×2×5;
它们的最小公倍数是:2×3×2×2×3×5=360.
分析:求两个数(或3个数)的最大公约数和最小公倍数,首先把每个数分解质因数,最大公约数是公有质因数的乘积;最小公倍数是公有质因数和各自独有的质因数连乘积;以此解答.
点评:此题主要考查求两个数或三个数的最大公约和最小公倍数的方法:两个数的公有质因数连乘积是最大公约数;两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;数字大的可以用短除法解答.
24=2×2×2×3;
36=2×2×3×3;
它们的最大公约数是:2×2×3=12;
最小公倍数是:2×2×3×2×3=72;
(2)18、24和40;
24=2×2×2×3;
18=2×3×3;
40=2×2×2×5;
它们的最小公倍数是:2×3×2×2×3×5=360.
分析:求两个数(或3个数)的最大公约数和最小公倍数,首先把每个数分解质因数,最大公约数是公有质因数的乘积;最小公倍数是公有质因数和各自独有的质因数连乘积;以此解答.
点评:此题主要考查求两个数或三个数的最大公约和最小公倍数的方法:两个数的公有质因数连乘积是最大公约数;两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;数字大的可以用短除法解答.

练习册系列答案
相关题目
口算
| 8400-8000= | 5000+300= | 35+24= | 70-34= |
| 36÷3= | 1500-500= | 86-39= | 37+46= |
| 55+19= | 3900-1900= | 96÷3= | 28÷2= |
| 84÷4= | 800+700= | 55÷5= | 48÷4= |