题目内容
 如图,已知梯形ABCD的面积是45平方米,高6米,底边BC长10米,三角形AED的面积是5平方米.求阴影部分的面积.
如图,已知梯形ABCD的面积是45平方米,高6米,底边BC长10米,三角形AED的面积是5平方米.求阴影部分的面积.分析:用梯形的面积减去三角形BCD和三角形AED的面积,先求三角形ABE的面积;然后根据S阴影=S△ABC-S△ABE,计算即可.
解答:解:S△ABE=梯形的面积-S△BCD-S△AED=45-10×6÷2-5=10(平方米);
S阴影=S△ABC-S△ABE=10×6÷2-10=20(平方米);
答:阴影部分的面积是20平方米;
S阴影=S△ABC-S△ABE=10×6÷2-10=20(平方米);
答:阴影部分的面积是20平方米;
点评:解答此题的关键:是用梯形的面积减去三角形BCD和三角形AED的面积,先求三角形ABE的面积;然后根据S阴影=S△ABC-S△ABE;应明确三角形的面积=底×高÷2.

练习册系列答案
相关题目
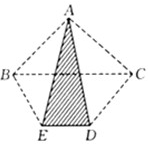 (2004?武汉)如图,已知△ABC的面积是2,梯形BCDE的面积是6,并且上底BC是下底DE的2倍,那么△ADE的面积是
(2004?武汉)如图,已知△ABC的面积是2,梯形BCDE的面积是6,并且上底BC是下底DE的2倍,那么△ADE的面积是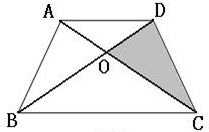 如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积?
如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积? 如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积?
如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积? 如图,已知△ABC的面积是2,梯形BCDE的面积是6,并且上底BC是下底DE的2倍,那么△ADE的面积是________.
如图,已知△ABC的面积是2,梯形BCDE的面积是6,并且上底BC是下底DE的2倍,那么△ADE的面积是________.