题目内容
17.有一个平行四边形,在上下两条边上个有一点,把这两点分别于对边的顶点连接,将平行四边形分成了如右图的七小块,其中四边形乙的面积是50平方厘米,三角形甲的面积是四边形乙的$\frac{2}{5}$,三角形丙的面积是30平方厘米.
分析 如下图:
假设三角形BGE的面积为a,三角形FGE的面积为b,三角形FEH的面积为c,三角形ECH的面积为d,因为四边形ABFE为梯形,所以三角形ABED的面积=三角形FEB的面积,即a+甲=a+b,所以甲=b,同理丙=c,由图可知,b+c=乙,所以甲+丙=乙,丙=乙-甲,代入数据即可求出乙的面积.
解答 解:由分析可知,丙的面积=乙的面积-甲的面积,
甲的面积为:50×$\frac{2}{5}$=20(平方厘米),
丙的面积为:50-20=30(平方厘米),
答:丙的面积为30平方厘米.
故答案为:30.
点评 本题主要考查了“同底等高三角形面积相等”这一性质的灵活应用,解题时注意辅助线添加要合理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.把10克盐放入90克水中,盐与盐水的质量比是( )
| A. | 1:9 | B. | 1:10 | C. | 10:1 |
5.能简算的要简算.
6.5×4+3.5×4-17;
87×$\frac{3}{86}$;
25×$\frac{1}{3}×\frac{2}{5}×\frac{3}{10}$;
26.35÷6.2+14.5.
6.5×4+3.5×4-17;
87×$\frac{3}{86}$;
25×$\frac{1}{3}×\frac{2}{5}×\frac{3}{10}$;
26.35÷6.2+14.5.
12.0.995保留一位小数是( )
| A. | 0.99 | B. | 1.00 | C. | 1.0 | D. | 0.1 |
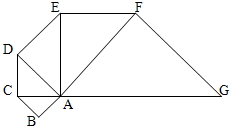 如图,以等腰直角三角形ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以等腰直角三角形ACD的斜边AD为直角边,画第三个等腰直角三角ADE,…,以此类推直到第五个等腰直角三角形AFG.已知,这五个等腰直角三角形的面积和为15.5,求原来等腰直角三角形ABC的直角边的长.
如图,以等腰直角三角形ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以等腰直角三角形ACD的斜边AD为直角边,画第三个等腰直角三角ADE,…,以此类推直到第五个等腰直角三角形AFG.已知,这五个等腰直角三角形的面积和为15.5,求原来等腰直角三角形ABC的直角边的长.