Question

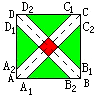这是一块正方形的地板砖示意图．其中AA1=AA2=BB1=BB2=CC1=CC2=DD1=DD2，红色小正方形的面积是4，绿色的四块面积总和是18．求这个大正方形ABCD的面积，请说明理由．

Answer 1

分析：如图，把大正方形的两条对角线把大正方形平均分成四个完全相同的等腰直角三角形，把左边的等腰直角三角形移到右边，与右边的正好组成一个正方形，则内部绿色的小正方形的面积是四块绿色面积的总和的一半，是18÷2=9，因为3×3=9，所以拼成的绿色正方形的边长是3，又因为中间红色小正方形的面积是4，则大正方形的两条对角线把红色小正方形平均分成四个完全相同的小正方形，每个红色小正方形的面积是4÷4=1，则红色小正方形的边长是1，据此可得出右边虚线围成的大正方形的边长，即可求出它的面积，再乘2就是原来大正方形的面积．

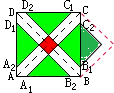
解答：解：根据题干分析可得：如上图所示，右边围成的绿色小正方形的面积是18÷2=9，
又因为3×3=9，所以绿色小正方形的边长是3；
中间红色小正方形的面积是4，则大正方形的两条对角线把红色小正方形平均分成四个完全相同的小正方形，每个红色小正方形的面积是4÷4=1，则红色小正方形的边长是1，
所以右边虚线围成的大正方形的边长是3+1+1=5，
则可得它的面积是5×5=25，
所以原正方形的面积是25×2=50．
答：大正方形ABCD的面积是50．

点评：解答此题的关键是明确大正方形的两条对角线把大正方形分成四个等腰直角三角形，再利用辅助线把其中的两个等腰直角三角形拼成一个新的正方形，根据已知的面积，求出它的边长即可解答问题．