题目内容
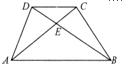
在梯形ABCD中，AD∥BC，AD=30，BC=50，AB=80，点P在线段AB上，且AP：PB=3：5，则角DPC为
直角
直角
（填写“锐角”，“直角”或“钝角”）分析：根据AP：PB=3：5，AB=80，，可得AP=30，BP=50，则三角形APD和PBC都是等腰三角形，再根据梯形的性质可得∠A+∠B=180度，依此可得加等于90度，，再根据平角=180°，即可求解．
解答：解：是直角
因为三角形APD和PBC都是等腰三角形，且∠A+∠B=180度，
两个底角相加等于90度，即∠APD+∠BPC=90度，
所以∠DPC=90度．
故答案为：直角．
因为三角形APD和PBC都是等腰三角形，且∠A+∠B=180度，
两个底角相加等于90度，即∠APD+∠BPC=90度，
所以∠DPC=90度．
故答案为：直角．
点评：考查了多边形的内角和，本题得到三角形APD和PBC都是等腰三角形是解题的关键．
练习册系列答案
相关题目
在梯形ABCD中，三角形AOD和三角形BOC的面积相比，（ ）大．
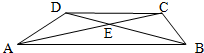如图，在梯形ABCD中，CD，AB分别是梯形的上底和下底，AC与BD交于点E，并设三角形ADE的面积是S1，三角形BCE的面积是S2，则（ ）
如图，在直角梯形ABCD中，AD∥BC，CD⊥BC，E为BC边上的点，将直角梯形ABCD沿对角线BD折叠，使△ABD与△EBD重合（如图中的阴影部分）．若∠A=120°，AB=4cm，求梯形ABCD的高CD．
如图，在梯形ABCD中，CD，AB分别是梯形的上底和下底，AC与BD交于点E，并设三角形ADE的面积是S1，三角形BCE的面积是S2，则