Question

是否在平面上存在这样的40条直线，它们共有365个交点？

Answer 1

分析：构造下面的直线：

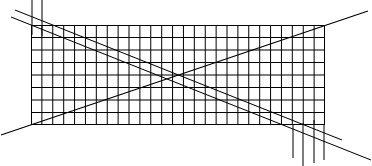
第一组A：28条线互相平行；
第二组B：9条线互相平行，且和第一组不平行；
第三组C：3条线只有两条是平行的，但和第一组第二组都不平行且第三条和第一组第二组不平行．

解答：解：可以办到．
40条直线平面上最多可以有1+2+…+39=780个交点．
如图所示：构造下面的直线：
第一组A：28条线互相平行；
第二组B：9条线互相平行，且和第一组不平行；
第三组C：3条线只有两条是平行的，但和第一组第二组都不平行且第三条和第一组第二组不平行．
AB交点数：28×9=252
AC交点数：28×3=84
BC交点数：9×3=27
C中的3条之间的交点数2
252+84+27+2=365个．

点评：本题还可以将围棋盘加上两条对角线，将棋盘的一组对边向外移动一格得到所求图形．