Question

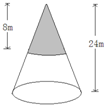把一个圆锥体按图切开，求切下的圆锥的体积与原圆锥体积比是

1：27

．

Answer 1

分析：圆锥的体积等于和它等底等高的圆柱体积的三分之一，因此有公式体积等于

1

3

πr²h，由图可得：切下的圆锥，它的高和半径都是原来圆锥的三分之一，根据公式就说明，切去的圆锥的体积是原来圆锥体积的

1

3

×

1

3

×

1

3

，即体积比是1：27；据此解答即可．

解答：解：由分析知：切下的圆锥，它的高和半径都是原来圆锥的三分之一，
切去的圆锥的体积是原来圆锥体积的

1

3

×

1

3

×

1

3

=

1

27

，即切下的圆锥的体积与原圆锥体积比1：27；
故答案为：1：27．

点评：此题考查了等底等高的圆锥和圆柱体积的关系，明确圆锥的体积等于和它等底等高的圆柱体积的三分之一，是解答本题的关键所在．