Question

小东和小华从甲、乙两地出发，往返于甲乙两地．已知小东的速度是小华的

4

5

，两人第一次相遇后，小东的速度提高30%，小华的速度提高20%，当两人再次相遇时发现两次相遇地点刚好相距230米．求甲、乙两地间的距离是多少米？

Answer 1

考点：多次相遇问题

专题：综合行程问题

分析：由于出发时小东的速度是小华的

4

5

，则第一次相遇时，小华行了全程的

5

4+5

=

5

9

，即相遇点与甲的距离为全程的

5

9

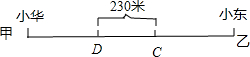
；第一次两人相遇于C点，第二次相遇于D点，第一次相遇，两人共走一个甲乙的路程；两人第一次相遇后，小东与小华的速度比为[

4

5

×（1+30%）]：[1×（1+20%）]=13：15，第一次相遇到第二次相遇，共走2个甲乙的路程，因此，小华应走全程的

4

9

+

15

15+13

×2=

191

126

，从而甲到D的距离是

191

126

-1=

65

126

，DC是

5

9

-

65

126

=

5

43

．已知DC是230千米，所以甲乙的长度是230÷

5

43

=1978（千米）

解答： 解：第一次相遇时，小华行了全程的

5

4+5

=

5

9

，
两人第一次相遇后，小东与小华的速度比为：[

4

5

×（1+30%）]：[1×（1+20%）]=1.04：1.2=13：15，
第一次相遇到第二次相遇，小华应走全程的

4

9

+

15

15+13

×2=

191

126

，
甲、乙两地间的距离是：
230÷[

5

9

-（

191

126

-1）]
=230÷[

5

9

-

65

126

]
=230÷

5

43

=1978（米）
答：甲、乙两地间的距离是1978米．

点评：此题解答的关键是求出第一次相遇时，小华行了全程的接分之几，然后求得两人第一次相遇后的速度比，同时明白第一次相遇到第二次相遇，共走2个甲乙的路程，进而解决问题．