题目内容
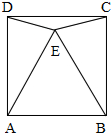如图，ABCD是正方形，△ABE是等边三角形，则∠DEC=（ ）度．| A、150 | B、120 | C、110 | D、100 |
分析：∠AED，∠BEC，∠AEB与∠DEC组成一个周角，根据已知分别求得∠AED，∠BEC，∠AEB的度数，从而利用周角是360度即可求得∠DCE的度数．
解答：解：因为四边形ABCD是正方形，
所以AB=BC，∠ABC=∠BCD=90°，
因为△ABE为等边三角形，
所以AE=AB=BE，∠AEB=∠AEB=60°，
所以∠EBC=90°-60°=30°，又因为BC=BE，
所以∠BEC=∠ECB=
（180°-30°）=75°，
同理，∠AED=75°
所以∠DEC=360°-75°-75°-60°=150°．
故选：A．
所以AB=BC，∠ABC=∠BCD=90°，
因为△ABE为等边三角形，
所以AE=AB=BE，∠AEB=∠AEB=60°，
所以∠EBC=90°-60°=30°，又因为BC=BE，
所以∠BEC=∠ECB=
| 1 |
| 2 |
同理，∠AED=75°
所以∠DEC=360°-75°-75°-60°=150°．
故选：A．
点评：此题主要考查了等边三角形和等腰三角形的性质，及正方形的性质．
练习册系列答案
相关题目
如图是一个公园的平面图，请按要求填空：