题目内容
 如图,已知四边形ABCD中,E、F分别是AD、BC的中点,连接AF、DF、BE、CE.△AFD面积为2,△BCE的面积为5,则四边形ABCD的面积为多少?
如图,已知四边形ABCD中,E、F分别是AD、BC的中点,连接AF、DF、BE、CE.△AFD面积为2,△BCE的面积为5,则四边形ABCD的面积为多少?分析:如图所示,连接AC,因为E为AD中点,所以在三角形ACD中S△ACE=S△DCE=
S△ACD;同理:S△ACF=S△ABF=
S△ABC所以四边形面积=S△ABC+S△ACD=2(S△ACE+S△ACF)=2S四边形AECF;连接EF,因为E为AD中点,所以在三角形AFD中,S△AEF=
S△AFD=1,同理:S△CEF=
S△BCE=
,所以S四边形AECF=S△AEF+S△CEF=
,所以就可以求出四边形ABCD的面积.

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |

解答:解:连接AC,因为E为AD中点,所以在三角形ACD中S△ACE=S△DCE=
S△ACD;
同理:S△ACF=S△ABF=
S△ABC所以四边形面积=S△ABC+S△ACD=2(S△ACE+S△ACF)=2S四边形AECF;
连接EF,因为E为AD中点,所以在三角形AFD中,S△AEF=
S△AFD=1,
同理:S△CEF=
S△BCE=
,
所以S四边形AECF=S△AEF+S△CEF=
,
所以四边形ABCD的面积为:2×S四边形AECF,
=2×
,
=7;
答:四边形ABCD的面积为7.
| 1 |
| 2 |
同理:S△ACF=S△ABF=
| 1 |
| 2 |
连接EF,因为E为AD中点,所以在三角形AFD中,S△AEF=
| 1 |
| 2 |
同理:S△CEF=
| 1 |
| 2 |
| 5 |
| 2 |
所以S四边形AECF=S△AEF+S△CEF=
| 7 |
| 2 |
所以四边形ABCD的面积为:2×S四边形AECF,
=2×
| 7 |
| 2 |
=7;
答:四边形ABCD的面积为7.
点评:解答此题的关键是:作出合适的辅助线,将要求的四边形的面积转化成与面积的图形有关的图形的面积.

练习册系列答案
相关题目
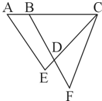 如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的
如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的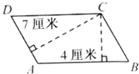 如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.
如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.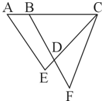 如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的________倍.
如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的________倍.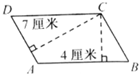 如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.
如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.