题目内容
 如图,有一个长6厘米,宽4厘米的长方形ABCD,已知线段DG、AH、AE、BF的长度依次是1,2,3,4厘米,且四边形AEPH的面积是5平方厘米,且四边形PFCG的面积是多少平方厘米?
如图,有一个长6厘米,宽4厘米的长方形ABCD,已知线段DG、AH、AE、BF的长度依次是1,2,3,4厘米,且四边形AEPH的面积是5平方厘米,且四边形PFCG的面积是多少平方厘米?分析:根据题干可以得出AH=CF=2厘米,AE=CG=3厘米,BF=DH=4厘米,
连接AP,CP.把该四边形分解为三角形进行解答.设△AHP在AH边上的高为x,△AEP在AE边上的高为y..然后得出四边形AEPH的面积=△AHP的面积+△AEP的面积.根据题意可求解
连接AP,CP.把该四边形分解为三角形进行解答.设△AHP在AH边上的高为x,△AEP在AE边上的高为y..然后得出四边形AEPH的面积=△AHP的面积+△AEP的面积.根据题意可求解

解答:解:连接AP,CP,设△AHP在AH边上的高为x厘米,△AEP在AE边上的高为y厘米,
则△CFP在CF边上的高为4-x厘米,△CGP在CG边上的高为6-y厘米,
根据题干分析可得:AH=CF=2厘米,AE=CG=3厘米,
四边形AEPH的面积=△AHP的面积+△AEP的面积,所以:
AH×x×12+AE×y×12,
2x×12+3y×12=5,
2x+3y=10,
四边形PFCG的面积=△CGP的面积+△CFP的面积:
CF×(4-x)×12+CG×(6-y)×
,
=2(4-x)×12+3(6-y)×
,
=(26-2x-3y)×
,
=(26-10)×
,
=8.
答:四边形PFCG的面积是8.
则△CFP在CF边上的高为4-x厘米,△CGP在CG边上的高为6-y厘米,
根据题干分析可得:AH=CF=2厘米,AE=CG=3厘米,
四边形AEPH的面积=△AHP的面积+△AEP的面积,所以:
AH×x×12+AE×y×12,
2x×12+3y×12=5,
2x+3y=10,
四边形PFCG的面积=△CGP的面积+△CFP的面积:
CF×(4-x)×12+CG×(6-y)×
| 1 |
| 2 |
=2(4-x)×12+3(6-y)×
| 1 |
| 2 |
=(26-2x-3y)×
| 1 |
| 2 |
=(26-10)×
| 1 |
| 2 |
=8.
答:四边形PFCG的面积是8.
点评:本题考查了对矩形的性质,三角形的面积等知识点,把四边形的面积分解为三角形的面积来求解是解此题的关键.

练习册系列答案
相关题目
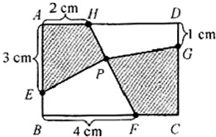 如图,有一个宽4厘米、长6厘米的长方形ABCD,在各个边上取点E、F、G、H,在连接H、F的线上取点P,连接EP和GP.当四边形AEPH的面积是5平方厘米时,求四边形PFCG的面积.
如图,有一个宽4厘米、长6厘米的长方形ABCD,在各个边上取点E、F、G、H,在连接H、F的线上取点P,连接EP和GP.当四边形AEPH的面积是5平方厘米时,求四边形PFCG的面积. 如图,在边长为6厘米的正方形内,有四个半径相等的圆,每相邻的两个圆仅有一个公共点,求阴影部分的面积为
如图,在边长为6厘米的正方形内,有四个半径相等的圆,每相邻的两个圆仅有一个公共点,求阴影部分的面积为 一天,村长给大家出了一道题:“如图,有一个棱长为5厘米的正方体木块,从它的每个面看都有一个穿透的完全相同的孔,你们谁能求出这个立体图形的表面积?”聪明的喜羊羊很快想到了方法:“(2×2×6)×8+(1×1×6)×12-4×12=216(平方厘米).”看着喜羊羊给出的答案,美羊羊和懒羊羊都目瞪口呆了,怎么也想不明白上面这道算式的意思,你能给他们解释一下吗?
一天,村长给大家出了一道题:“如图,有一个棱长为5厘米的正方体木块,从它的每个面看都有一个穿透的完全相同的孔,你们谁能求出这个立体图形的表面积?”聪明的喜羊羊很快想到了方法:“(2×2×6)×8+(1×1×6)×12-4×12=216(平方厘米).”看着喜羊羊给出的答案,美羊羊和懒羊羊都目瞪口呆了,怎么也想不明白上面这道算式的意思,你能给他们解释一下吗?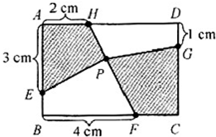 如图,有一个宽4厘米、长6厘米的长方形ABCD,在各个边上取点E、F、G、H,在连接H、F的线上取点P,连接EP和GP.当四边形AEPH的面积是5平方厘米时,求四边形PFCG的面积.
如图,有一个宽4厘米、长6厘米的长方形ABCD,在各个边上取点E、F、G、H,在连接H、F的线上取点P,连接EP和GP.当四边形AEPH的面积是5平方厘米时,求四边形PFCG的面积.