Question

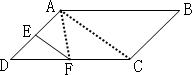
如图，平行四边形ABCD的面积是128平方厘米，E、F分别是AD、CD的中点，那么平行四边形ABCD的面积是三角形DEF面积的

8

倍．

Answer 1

分析：如下图所示，连接AC，AF，由等底等高的三角形面积相等，可知△DEF的面积等于△AEF的面积，都等于△ADF的面积的

1

2

，；△ADF的面积等于△ACF的面积，都等于△ADC面积的

1

2

，而△ADC的面积又等于平行四边形ABCD的面积的

1

2

，因此可以判断，三角形DEF面积是平行四边形ABCD的面积的

1

2

×

1

2

×

1

2

=

1

8

，因此平行四边形ABCD的面积是三角形DEF面积的8倍．

解答：解：如图，连接AC，AF．
因为等底等高的三角形面积相等，
所以△DEF的面积=△AEF的面积=△ADF的面积的

1

2

，
△DEF的面积=△AEF的面积=△ADC面积的

1

2

，
而△ADC的面积=平行四边形ABCD的面积的

1

2

，
因此，平行四边形ABCD的面积是三角形DEF面积的

1

2

×

1

2

×

1

2

=

1

8

，
所以，平行四边形ABCD的面积是三角形DEF面积的8倍．

点评：解决本题的关键是由等底等高的三角形的面积相等得出各三角形的面积之间的关系．