题目内容
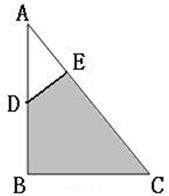
 如图:已知三角形ABC的面积是15平方厘米,BD:DC=AD:ED=2:1,求阴影部分的面积.
如图:已知三角形ABC的面积是15平方厘米,BD:DC=AD:ED=2:1,求阴影部分的面积.
解:S△DCF的面积=15÷5=3(平方厘米).
阴影部分面积等于△BDF的面积=△DCF的面积×2=3×2=6(平方厘米);
答:阴影部分的总面积是6平方厘米.
分析:连接DF,因为AD:ED=2:1,所以AE=DE,△AEF的面积=△EDF的面积,△ABE的面积=△BDE的面积.因为BD:DC2:1,所以△BDF的面积=△DCF的面积×2,因此△ABF的面积=△BDF的面积=△DCF的面积×2;所以△ABC的面积=△DCF的面积×5,于是△DCF的面积=15÷5=3(平方厘米).阴影部分面积等于△BDF的面积=△DCF的面积×2=3×2=6(平方厘米)

点评:解答此题的关键是先连接DF,然后根据高一定时,三角形面积和底的正比关系进行分析,进而得出结论.
阴影部分面积等于△BDF的面积=△DCF的面积×2=3×2=6(平方厘米);
答:阴影部分的总面积是6平方厘米.
分析:连接DF,因为AD:ED=2:1,所以AE=DE,△AEF的面积=△EDF的面积,△ABE的面积=△BDE的面积.因为BD:DC2:1,所以△BDF的面积=△DCF的面积×2,因此△ABF的面积=△BDF的面积=△DCF的面积×2;所以△ABC的面积=△DCF的面积×5,于是△DCF的面积=15÷5=3(平方厘米).阴影部分面积等于△BDF的面积=△DCF的面积×2=3×2=6(平方厘米)

点评:解答此题的关键是先连接DF,然后根据高一定时,三角形面积和底的正比关系进行分析,进而得出结论.

练习册系列答案
相关题目
 如图,已知等腰三角形ABC,D为AC中点,AB=BC=2厘米,
如图,已知等腰三角形ABC,D为AC中点,AB=BC=2厘米,

 如图,已知三角形ABC的面积为15平方厘米,D为AB边中点,E为AC边三等分点,求图中阴影部分面积?
如图,已知三角形ABC的面积为15平方厘米,D为AB边中点,E为AC边三等分点,求图中阴影部分面积?
 如图,已知三角形ABC的面积为15平方厘米,D为AB边中点,E为AC边三等分点,求图中阴影部分面积?
如图,已知三角形ABC的面积为15平方厘米,D为AB边中点,E为AC边三等分点,求图中阴影部分面积?