题目内容
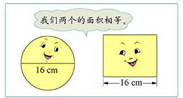
一个正方形和一个圆形的面积相等,正方形的边长一定大于圆的半径.______.(判断对错)
假设圆的半径为r,
则圆的面积=πr2,
则正方形的面积=πr2,
因为π>1,
所以正方形的边长>r,
所以一个正方形和一个圆形的面积相等,正方形的边长一定大于圆的半径.
故答案为:√.
则圆的面积=πr2,
则正方形的面积=πr2,
因为π>1,
所以正方形的边长>r,
所以一个正方形和一个圆形的面积相等,正方形的边长一定大于圆的半径.
故答案为:√.

练习册系列答案
相关题目