Question

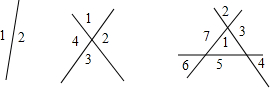
一条直线把平面分成两部分，两条直线把平面分成四部分，三条直线把平面分成七部分，…

直线条数	1	2	3	4	5	…
分成的部分	2	4	7	11	16	…

根据规律求10条直线把平面分成几部分？

Answer 1

考点：组合图形的计数

专题：几何的计算与计数专题

分析：根据一条直线、两条直线、三条直线的情况可总结出规律，从而可得出答案．

解答： 解：由图可知，
（1）有一条直线时，最多分成2=

1×2

2

+1部分；
（2）有两条直线时，最多分成2+2=4=

2×3

2

+1部分；
（3）有三条直线时，最多分成1+1+2+3=7=

3×4

2

+1部分；…

（4）设直线条数有n条，分成的平面最多有m个．有以下规律：
m=1+1+…+（n-1）+n=

n(n+1)

2

+1．
所以画10条直线最多可将平面分成

10×11

2

+1=56．
答：10条直线把平面分成56部分．

点评：本题考查直线与平面的关系，有一定难度，注意培养由特殊到一般再到特殊的探究意识．