Question

13．如图，ABCD是一个平行四边形，E是AD边上任意一点，你能证明三角形BCE的面积是平行四边形的一半吗？试一试

Answer 1

分析 由点E是平行四边形ABCD中边AD上的任意一点，可得△BCE与?ABCD等底等高，根据平行四边形的面积=底×高，三角形的面积=底×高÷2，继而可得S_△BCE=S_?ABCD×$\frac{1}{2}$，解答即可．

解答 解：如图：过E点作EF垂直BC，垂足为F，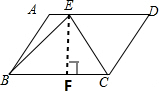

因为S?ABCD=BC×EF
S△BCE=$\frac{1}{2}$BC×EF
所以S△BCD：S?ABCD=$\frac{1}{2}$BC×EF：BC×EF=$\frac{1}{2}$
即三角形BCE的面积是平行四边形的一半．

点评 此题考查了平行四边形的性质．注意△EBC与?ABCD等底等高．