题目内容
列式计算.
① 的倒数与0.25的倒数的积是多少
的倒数与0.25的倒数的积是多少
②最小质数的倒数减去最小合数的倒数,所得的差的倒数是多少?
③ 与
与 的和乘它的差是多少?
的和乘它的差是多少?
④ 的倒数与
的倒数与 的倒数的和除以
的倒数的和除以 的倒数,是多少?
的倒数,是多少?
解:①1÷ ×(1÷0.25),
×(1÷0.25),
=2×4,
=8;
答:积是8.
②1÷(1÷2-1÷4),
=1÷( -
- ),
),
=1÷ ,
,
=4;
答:所得的差的倒数是4.
③( +
+ )×(
)×( -
- ),
),
=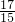 ×
×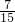 ,
,
= ;
;
答: 与
与 的和乘它的差是
的和乘它的差是 .
.
④(1÷ +1÷
+1÷ )÷(1÷
)÷(1÷ ),
),
=( +2)÷4,
+2)÷4,
= ×
× ,
,
= ;
;
答:是 .
.
分析:①求积,就要知道两个因数分别是多少.根据题意,一个是1÷ ,另一个是(1÷0.25),由此列式为1÷
,另一个是(1÷0.25),由此列式为1÷ ×(1÷0.25)计算即可;
×(1÷0.25)计算即可;
②最小的质数是2,最小的和数是4,根据倒数的概念,解决问题;
③写出 与
与 的和与差,相乘即可;
的和与差,相乘即可;
④写出 的倒数与
的倒数与 的倒数和,然后除以
的倒数和,然后除以 的倒数即可.
的倒数即可.
点评:完成此题,要注意条件中“积、减去、差、乘”等此类体现数据之间关系及运算顺序的关键词,以及倒数的概念.
 ×(1÷0.25),
×(1÷0.25),=2×4,
=8;
答:积是8.
②1÷(1÷2-1÷4),
=1÷(
 -
- ),
),=1÷
 ,
,=4;
答:所得的差的倒数是4.
③(
 +
+ )×(
)×( -
- ),
),=
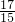 ×
×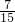 ,
,=
 ;
;答:
 与
与 的和乘它的差是
的和乘它的差是 .
.④(1÷
 +1÷
+1÷ )÷(1÷
)÷(1÷ ),
),=(
 +2)÷4,
+2)÷4,=
 ×
× ,
,=
 ;
;答:是
 .
.分析:①求积,就要知道两个因数分别是多少.根据题意,一个是1÷
 ,另一个是(1÷0.25),由此列式为1÷
,另一个是(1÷0.25),由此列式为1÷ ×(1÷0.25)计算即可;
×(1÷0.25)计算即可;②最小的质数是2,最小的和数是4,根据倒数的概念,解决问题;
③写出
 与
与 的和与差,相乘即可;
的和与差,相乘即可;④写出
 的倒数与
的倒数与 的倒数和,然后除以
的倒数和,然后除以 的倒数即可.
的倒数即可.点评:完成此题,要注意条件中“积、减去、差、乘”等此类体现数据之间关系及运算顺序的关键词,以及倒数的概念.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的和乘4与
的和乘4与 的差,积是多少?
的差,积是多少?