题目内容
利用单摆测定重力加速度试验中，若测得的g值偏小，可能的原因是（ ）
|
试题答案
BCD| A．摆球在水平面上作圆周运动 |
| B．测摆长时，仅测了线长，未加小球半径 |
| C．测周期时，把n次全振动误记为（n-1）次 |
| D．摆球上端未固定牢固，振动中出现松动 |
A．摆球在水平面上作圆周运动
B．测摆长时，仅测了线长，未加小球半径
C．测周期时，把n次全振动误记为（n-1）次
D．摆球上端未固定牢固，振动中出现松动
查看习题详情和答案>>
在利用单摆测定重力加速度的实验中，一位学生在不同摆长l的条件下，测得单摆的周期T与摆长l的关系如下| 次数 | 1 | 2 | 3 | 4 | 5 |
| L（m） | 0.8000 | 0.9000 | 1.0000 | 1.1000 | 1.2000 |
| T（s） | 1.80 | 1.90 | 2.01 | 2.11 | 2.20 |
| T2（s2） | 3.24 | 3.61 | 4.04 | 4.45 | 4.84 |
①写出利用图线求重力加速度的公式，g=
②由图线计算出的重力加速度的值g=
在利用单摆测定重力加速度的实验中，一位学生在不同摆长l的条件下，测得单摆的周期T与摆长l的关系如下：
试在坐标纸上画出T2与l的关系图线，写出利用图线求重力加速度的公式，g＝________．计算出的重力加速度的值，ｇ＝________m/s2．(保留3位有效数字)
（1）为了减小测量周期的误差，计时开始时，摆球应是经过最
（2）用主尺最小分度为1mm，游标上有20个分度的卡尺测量金属球的直径，结果如图乙所示，可以读出此金属球的直径为D=
（3）为了提高实验精度，在试验中可改变几次摆长l，测出相应的周期T，从而得出一组对应的l和T的数值，再以l为横坐标T2为纵坐标，将所得数据连成直线如图丙所示，利用图线的斜率k可求出重力加速度的表达式为g=
在“用单摆测定重力加速度”的实验中：
(1)为了减小测量周期的误差，计时开始时，摆球应是经过最 （填“高”或“低”）点的位置，且用秒表测量单摆完成多次次全振动所用的时间，秒表的示数如图甲所示，则秒表的示数为t= s
(2）用主尺最小分度为1mm，游标上有20个分度的卡尺测量金属球的直径，结果如图乙所示，可以读出此金属球的直径为D=________mm。
（3）为了提高实验精度，在试验中可改变几次摆长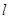
，测出相应的周期Ｔ，从而得出一组对应的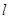和T的数值，再以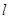为横坐标T2为纵坐标，将所得数据连成直线如图所示，利用图线的斜率
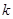可求出重力加速度的表达式为
= ，可求得= m/s2。（保留三位有效数字）
在“用单摆测定重力加速度”的实验中：
(1)为了减小测量周期的误差，计时开始时，摆球应是经过最 （填“高”或“低”）点的位置，且用秒表测量单摆完成多次次全振动所用的时间，秒表的示数如图甲所示，则秒表的示数为t= s
(2）用主尺最小分度为1mm，游标上有20个分度的卡尺测量金属球的直径，结果如图乙所示，可以读出此金属球的直径为D=________mm。
（3）为了提高实验精度，在试验中可改变几次摆长
，测出相应的周期Ｔ，从而得出一组对应的和T的数值，再以为横坐标T2为纵坐标，将所得数据连成直线如图所示，利用图线的斜率
可求出重力加速度的表达式为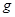
= ，可求得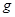= m/s2。（保留三位有效数字）
查看习题详情和答案>>
(1)为了减小测量周期的误差，计时开始时，摆球应是经过最 （填“高”或“低”）点的位置，且用秒表测量单摆完成多次次全振动所用的时间，秒表的示数如图甲所示，则秒表的示数为t= s
(2）用主尺最小分度为1mm，游标上有20个分度的卡尺测量金属球的直径，结果如图乙所示，可以读出此金属球的直径为D=________mm。
（3）为了提高实验精度，在试验中可改变几次摆长
，测出相应的周期Ｔ，从而得出一组对应的和T的数值，再以为横坐标T2为纵坐标，将所得数据连成直线如图所示，利用图线的斜率
可求出重力加速度的表达式为
= ，可求得= m/s2。（保留三位有效数字）
（1）用毫米刻度尺测量摆线的长时，将摆线平放，如图（A）所示，刻度尺读数是
（2）该同学用秒表记录了单摆振动30次全振动所用的时间如图C所示，则秒表所示读数为
（3）为了提高实验精度，在试验中可改变几次摆长L，测出相应的周期T，从而得出一组对应的L与T的数值，再以L为横坐标T2为纵坐标，将所得数据连成直线如图D所示，利用图线可求出g=