题目内容
如图所示,足够长的水平传送带以速度v沿逆时针方向转动,传送带的左端与光滑圆弧轨道底部平滑连接,圆弧轨道上的A点与圆心等高,一小物块从A点静止滑下,再滑上传送带,经过一段时间又返回圆弧轨道,返回圆弧轨道时小物块恰好能到达A点,则下列说法正确的是( )
 |
试题答案
BD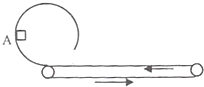 如图所示,足够长的水平传送带以速度v沿逆时针方向转动,传送带的左端与光滑圆弧轨道底部平滑连接,圆弧轨道上的A点与圆心等高,一小物块从A点静止滑下,再滑上传送带,经过一段时间又返回圆弧轨道,返回圆弧轨道时小物块恰好能到达A点,则下列说法正确的是( )
如图所示,足够长的水平传送带以速度v沿逆时针方向转动,传送带的左端与光滑圆弧轨道底部平滑连接,圆弧轨道上的A点与圆心等高,一小物块从A点静止滑下,再滑上传送带,经过一段时间又返回圆弧轨道,返回圆弧轨道时小物块恰好能到达A点,则下列说法正确的是( ) 如图所示,足够长的水平传送带以速度v沿逆时针方向转动,传送带的左端与光滑圆弧轨道底部平滑连接,圆弧轨道上的A点与圆心等高,一小物块从A点静止滑下,再滑上传送带,经过一段时间又返回圆弧轨道,返回圆弧轨道时小物块恰好能到达A点,则下列说法正确的是( )
如图所示,足够长的水平传送带以速度v沿逆时针方向转动,传送带的左端与光滑圆弧轨道底部平滑连接,圆弧轨道上的A点与圆心等高,一小物块从A点静止滑下,再滑上传送带,经过一段时间又返回圆弧轨道,返回圆弧轨道时小物块恰好能到达A点,则下列说法正确的是( )A、圆弧轨道的半径可能是
| ||
| B、若减小传送带速度,则小物块不可能到达A点 | ||
| C、若增加传送带速度,则小物块有可能经过圆弧轨道的最高点 | ||
| D、不论传送带速度增加到多大,小物块都不可能经过圆弧轨道的最高点 |
| A.圆弧轨道的半径一定是v2/2g |
| B.若减小传送带速度,则小物块仍有可能到达A |
| C.若增加传送带速度,则小物块有可能经过圆弧轨道的最高点 |
| D.不论传送带速度增加到多大,小物块都不可能经过圆弧轨道的最高点 |


如图所示,足够长的水平传送带以速度v沿逆时针方向转动,传送带的左端与光滑圆弧轨道底部平滑连接,圆弧轨道上的A点与圆心等高,一小物块从A点静止滑下,再滑上传送带,经过一段时间又返回圆弧轨道,返回圆弧轨道时小物块恰好能到达A点,则下列说法正确的是

A.圆弧轨道的半径一定是v2/2 g
B.若减小传送带速度,则小物块仍有可能到达A
C.若增加传送带速度,则小物块有可能经过圆弧轨道的最高点
D.不论传送带速度增加到多大,小物块都不可能经过圆弧轨道的最高点
如图所示,足够长的水平传送带始终以v=3m/s的速度沿逆时针方向运动,传送带上有一质量M=2kg的小木盒A,A与传送带之间的动摩擦因数![]() =0.3,开始时,A与传送带保持相对静止。先后相隔△t=3s有两个光滑的、质量m=1kg的小球B自传送带的左端出发,以v0=15m/s的速度在传送带上向右运动,第1个球与木盒相遇后立即进入盒中并与盒保持相对静止,第2个球出发后历时△t1=
=0.3,开始时,A与传送带保持相对静止。先后相隔△t=3s有两个光滑的、质量m=1kg的小球B自传送带的左端出发,以v0=15m/s的速度在传送带上向右运动,第1个球与木盒相遇后立即进入盒中并与盒保持相对静止,第2个球出发后历时△t1=![]() s与木盒相遇,取g=10m/s2,求:
s与木盒相遇,取g=10m/s2,求:

(1)第1个球与木盒相遇后瞬间,两者共同运动的速度v1.
(2)第1个球自出发到与木盒相遇所需的时间t0。
(3)在木盒与第1个球相遇至与第2个球相遇的过程中,由于木盒与传送带间的摩擦而产生的热量Q。
查看习题详情和答案>>


