例1 作下列函数的简图
(1)y=sinx,x∈[0,2π], (2)y=cosx,x∈[0,2π],
(3)y=1+sinx,x∈[0,2π], (4)y=-cosx,x∈[0,2π],
 解:(1)列表
解:(1)列表
|
X |
0 |
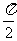 |
 |
 |
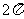 |
|
Sinx |
0 |
1 |
0 |
-1 |
0 |
(2)列表
|
X |
0 |
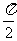 |
 |
 |
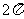 |
|
Cosx |
1 |
0 |
-1 |
0 |
1 |
(3)列表
|
X |
0 |
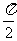 |
 |
 |
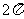 |
|
Sinx |
0 |
1 |
0 |
-1 |
0 |
|
1+sinx |
1 |
2 |
1 |
0 |
1 |
(4)列表
|
X |
0 |
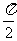 |
 |
 |
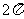 |
|
Cosx |
1 |
0 |
-1 |
0 |
1 |
|
-cosx |
-1 |
0 |
1 |
0 |
-1 |
例2 利用正弦函数和余弦函数的图象,求满足下列条件的x的集合:

解:作出正弦函数y=sinx,x∈[0,2π]的图象:
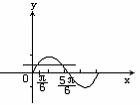
由图形可以得到,满足条件的x的集合为: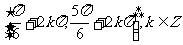
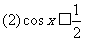
解:作出余弦函数y=cos,x∈[0,2π]的图象:
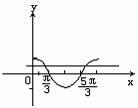
由图形可以得到,满足条件的x的集合为:

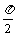 ,1) (p,0) (
,1) (p,0) (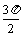 ,-1) (2p,0)
,-1) (2p,0) (3)也同样可用五点法作图:y=cosx xÎ[0,2p]的五个点关键是
(3)也同样可用五点法作图:y=cosx xÎ[0,2p]的五个点关键是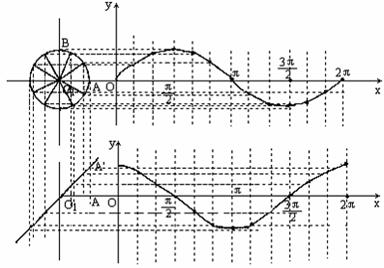
 ,以
,以 ,
,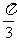 ,
,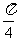 角的直线,
角的直线,

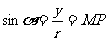 ,
,
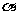 是一个任意角,在
是一个任意角,在
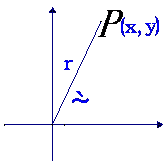 比值
比值 叫做
叫做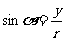
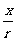 叫做
叫做
 叫做
叫做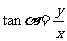
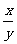 叫做
叫做
 叫做
叫做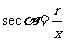
 叫做
叫做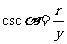
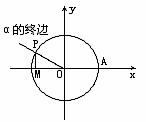 二、讲解新课:
二、讲解新课: