8.抛物线的标准方程及其几何性质:
|
标准方程 |
 |
 |
 |
 |
|
|
图形 |
 |
 |
 |
 |
|
|
对称轴 |
 轴 轴 |
 轴 轴 |
 轴 轴 |
 轴 轴 |
|
|
焦点 |
 |
 |
 |
 |
|
|
顶点 |
原点 |
||||
|
准线 |
 |
 |
 |
 |
|
|
离心率 |
 1 1 |
||||

 与半椭圆
与半椭圆
 合成的曲线称作“果圆”,其中
合成的曲线称作“果圆”,其中 ,
, ,
, .
.  ,
, ,
, 是相应椭圆的焦点,
是相应椭圆的焦点, ,
, 和
和 ,
, 是“果圆” 与
是“果圆” 与 ,
, 轴的交点,
轴的交点,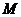 是线段
是线段 的中点.
的中点. (1)若
(1)若 是边长为1的等边三角形,求该
是边长为1的等边三角形,求该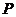 是“果圆”的半椭圆
是“果圆”的半椭圆 取得最小值时,
取得最小值时, 或
或 处;
处;
 ,
, ,
, ,
, ,
, .
.  ,则
,则
 ,
,  ,
,
 的最小值只能在
的最小值只能在 或
或 处取到.
处取到. ,且
,且 和
和 同时位于“果圆”的半椭圆
同时位于“果圆”的半椭圆 和半椭圆
和半椭圆 上,所以,由(2)知,只需研究
上,所以,由(2)知,只需研究 上的情形即可.
上的情形即可.  .
. ,即
,即 时,
时, 时取到,
时取到, .
.
 ,即
,即 时,由于
时,由于 时是递减的,
时是递减的, 时取到,此时
时取到,此时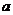 .
.
 取得最小值时,点
取得最小值时,点 .
. 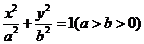 的两个焦点为F1,F2,点P在椭圆C上,且
的两个焦点为F1,F2,点P在椭圆C上,且
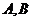 两点,且A、B关于点M对称,求直线l的方程.
两点,且A、B关于点M对称,求直线l的方程. ,a=3.
,a=3. 故椭圆的半焦距c=
故椭圆的半焦距c= ,
, =1.
=1.
 ,
,
 x2且
x2且 ①
① ②
② ③
③ =
= ,
, 、
、 、
、 .
. ,直线与圆锥曲线的两个交点坐标分别为
,直线与圆锥曲线的两个交点坐标分别为 ,则它的弦长
,则它的弦长
 ,运用韦达定理来进行计算.
,运用韦达定理来进行计算. .
. (看作点的集合或适合某种条件的点的轨迹)上的点与一个二元方程
(看作点的集合或适合某种条件的点的轨迹)上的点与一个二元方程 的实数解建立了如下的关系:
的实数解建立了如下的关系:
 上).定点F叫做抛物线的焦点, 定直线
上).定点F叫做抛物线的焦点, 定直线