21.(本小题满分12分)
已知函数 ,其中
,其中


(1) 当 满足什么条件时,
满足什么条件时,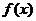 取得极值?
取得极值?
(2) 已知 ,且
,且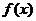 在区间
在区间 上单调递增,试用
上单调递增,试用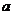 表示出
表示出 的取值范围.
的取值范围.
解: (1)由已知得 ,令
,令 ,得
,得 ,
,
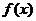 要取得极值,方程
要取得极值,方程 必须有解,
必须有解,
所以△ ,即
,即 , 此时方程
, 此时方程 的根为
的根为
 ,
, ,
,
所以


当 时,
时,
|
x |
(-∞,x1) |
x 1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
f’(x) |
+ |
0 |
- |
0 |
+ |
|
f (x) |
增函数 |
极大值 |
减函数 |
极小值 |
增函数 |
所以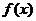 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
当 时,
时, 

|
x |
(-∞,x2) |
x 2 |
(x2,x1) |
x1 |
(x1,+∞) |
|
f’(x) |
- |
0 |
+ |
0 |
- |
|
f (x) |
减函数 |
极小值 |
增函数 |
极大值 |
减函数 |
所以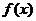 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
综上,当 满足
满足 时,
时, 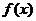 取得极值.
取得极值. 

(2)要使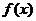 在区间
在区间 上单调递增,需使
上单调递增,需使 在
在 上恒成立.
上恒成立.
即 恒成立, 所以
恒成立, 所以
设 ,
, ,
,
令 得
得 或
或 (舍去),
(舍去), 

当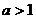 时,
时, ,当
,当 时
时 ,
, 单调增函数;
单调增函数;
当 时
时 ,
, 单调减函数,
单调减函数,
所以当 时,
时, 取得最大,最大值为
取得最大,最大值为 .
.
所以
当 时,
时, ,此时
,此时 在区间
在区间 恒成立,所以
恒成立,所以 在区间
在区间 上单调递增,当
上单调递增,当 时
时 最大,最大值为
最大,最大值为 ,所以
,所以
综上,当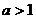 时,
时,  ; 当
; 当 时,
时, 


[命题立意]:本题为三次函数,利用求导的方法研究函数的极值、单调性和函数的最值,函数在区间上为单调函数,则导函数在该区间上的符号确定,从而转为不等式恒成立,再转为函数研究最值.运用函数与方程的思想,化归思想和分类讨论的思想解答问题.
19. (本小题满分12分)
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
|
|
轿车A |
轿车B |
轿车C |
|
舒适型 |
100 |
150 |
z |
|
标准型 |
300 |
450 |
600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1) 求z的值. 

(2) 用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3) 用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
解: (1).设该厂本月生产轿车为n辆,由题意得, ,所以n=2000. z=2000-100-300-150-450-600=400
,所以n=2000. z=2000-100-300-150-450-600=400
(2) 设所抽样本中有m辆舒适型轿车,因为用分层抽样的方法在C类轿车中抽取一个容量为5的样本,所以 ,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,则从中任取2辆的所有基本事件为(S1, B1), (S1, B2) , (S1,
B3) (S2 ,B1), (S2 ,B2), (S2
,B3),( (S1, S2),(B1 ,B2),
(B2 ,B3) ,(B1 ,B3)共10个,其中至少有1辆舒适型轿车的基本事件有7个基本事件: (S1, B1),
(S1, B2) , (S1, B3) (S2 ,B1),
(S2 ,B2), (S2 ,B3),( (S1,
S2),所以从中任取2辆,至少有1辆舒适型轿车的概率为
,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,则从中任取2辆的所有基本事件为(S1, B1), (S1, B2) , (S1,
B3) (S2 ,B1), (S2 ,B2), (S2
,B3),( (S1, S2),(B1 ,B2),
(B2 ,B3) ,(B1 ,B3)共10个,其中至少有1辆舒适型轿车的基本事件有7个基本事件: (S1, B1),
(S1, B2) , (S1, B3) (S2 ,B1),
(S2 ,B2), (S2 ,B3),( (S1,
S2),所以从中任取2辆,至少有1辆舒适型轿车的概率为 .
.
(3)样本的平均数为 ,
,
那么与样本平均数之差的绝对值不超过0.5的数为9.4, 8.6, 9.2, 8.7, 9.3, 9.0这6个数,总的个数为8,所以该数与样本平均数之差的绝对值不超过0.5的概率为 .
.
[命题立意]:本题为概率与统计的知识内容,涉及到分层抽样以及古典概型求事件的概率问题.要读懂题意,分清类型,列出基本事件,查清个数.,利用公式解答.
 是函数
是函数 的反函数,且
的反函数,且 ,则
,则
 B.
B. C.
C. D.2
D.2
 ,又
,又 ,
, ,故
,故 ,选A.
,选A. ,b=
,b= , 则向量
, 则向量
 轴
B.平行于第一、三象限的角平分线
轴
B.平行于第一、三象限的角平分线  轴
D.平行于第二、四象限的角平分线
轴
D.平行于第二、四象限的角平分线  ,由
,由 及向量的性质可知,C正确.
及向量的性质可知,C正确. =1(i是虚数单位)的是
=1(i是虚数单位)的是  ,故选C.
,故选C.  +x=0} 关系的韦恩(Venn)图是
+x=0} 关系的韦恩(Venn)图是 
 得
得 ,选B.
,选B. ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量 ,向量
,向量 ,
, ,动点
,动点 的轨迹为E.
的轨迹为E. ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;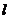 与圆C:
与圆C: (1<R<2)相切于A1,且
(1<R<2)相切于A1,且 , 即
, 即 .
. ;
; 时, 方程表示的是圆
时, 方程表示的是圆 且
且 时,方程表示的是椭圆;
时,方程表示的是椭圆;  时,方程表示的是双曲线.
时,方程表示的是双曲线. ,设圆心在原点的圆的一条切线为
,设圆心在原点的圆的一条切线为 ,解方程组
,解方程组 得
得 ,即
,即 ,
, ,
, ,即
,即 ,
且
,
且
 ,
, , 需使
, 需使 ,即
,即 ,
, , 即
, 即 且
且 恒成立.
恒成立. ,
, , 所求的圆为
, 所求的圆为 .
. ,与
,与 或
或 也满足
也满足 , 即
, 即 ①,
①, , 即
, 即 ,
②
,
② , 此时A,B重合为B1(x1,y1)点,
, 此时A,B重合为B1(x1,y1)点, ,所以,
,所以, ,
,  ,所以
,所以 ,
, 因为
因为 当且仅当
当且仅当 时取等号,所以
时取等号,所以 ,即
,即 }的前n项和为
}的前n项和为 , 已知对任意的
, 已知对任意的 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.
均为常数)的图像上.  求数列
求数列 的前
的前 项和
项和
 ,
, 时,
时, ,
,  时,
时, ,
, , 公比为
, 公比为
 ,
, 






 如图,在直四棱柱ABCD-A
如图,在直四棱柱ABCD-A B
B 连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD, 平面FCC
平面FCC 平面FCC
平面FCC (2)连接AC,在直棱柱中,CC1⊥平面ABCD,AC
(2)连接AC,在直棱柱中,CC1⊥平面ABCD,AC 平面ABCD,
平面ABCD, ,△ACF为等腰三角形,且
,△ACF为等腰三角形,且
 平面D1AC,
平面D1AC, 在
在 处取最小值.
处取最小值. .的值;
.的值; ABC中,
ABC中, 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知
 ,求角C..
,求角C..



 ,由诱导公式知
,由诱导公式知 ,因为
,因为 ,所以
,所以 .所以
.所以
 ,因为角A为
,因为角A为 .又因为
.又因为 ,也就是
,也就是 ,
, ,所以
,所以 或
或 .
. ;当
;当 .
.