摘要:教材把指数函数.对数函数.幂函数当作三种重要的函数模型来学习.强调通过实例和图象的直观.揭示这三种函数模型增长的差异及其关系.体会建立和研究一个函数模型的基本过程和方法.学会运用具体函数模型解决一些实际问题.1. 了解指数函数模型的实际背景.
网址:http://m.1010jiajiao.com/timu_id_4460181[举报]
我们知道,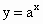 (0<a≠1)与
(0<a≠1)与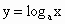 (0<a≠1)互为反函数,只要把同底的指数函数与对数函数的解析式互化,就可以由其中的一个得到它的反函数的解析式.仿此,请探究函数y=2x+1是否有反函数.如果有,你能否求出反函数?
(0<a≠1)互为反函数,只要把同底的指数函数与对数函数的解析式互化,就可以由其中的一个得到它的反函数的解析式.仿此,请探究函数y=2x+1是否有反函数.如果有,你能否求出反函数?
我们知道,
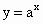 (0<a≠1)与
(0<a≠1)与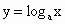 (0<a≠1)互为反函数,只要把同底的指数函数与对数函数的解析式互化,就可以由其中的一个得到它的反函数的解析式.仿此,请探究函数y=2x+1是否有反函数.如果有,你能否求出反函数?
查看习题详情和答案>>
(0<a≠1)互为反函数,只要把同底的指数函数与对数函数的解析式互化,就可以由其中的一个得到它的反函数的解析式.仿此,请探究函数y=2x+1是否有反函数.如果有,你能否求出反函数?
查看习题详情和答案>>
某商场经营一批进价为12元/个的小商品.在4天的试销中,对此商品的单价x(元)与相应的日销量y(个)作了统计,其数据如表
(1)能否找到一种函数,使它反映y关于x的函数关系?若能,写出函数解析式;(提示:可根据表格中的数据描点后观察,再从一次函数,二次函数,指数函数,对数函数等中选择)
(2)设经营此商品的日销售利润为P(元),求P关于x的函数解析式,并指出当此商品的销售价每个为多少元时,才能使日销售利润P取最大值?最大值是多少?
查看习题详情和答案>>
| x | 16 | 20 | 24 | 28 |
| y | 42 | 30 | 18 | 6 |
(2)设经营此商品的日销售利润为P(元),求P关于x的函数解析式,并指出当此商品的销售价每个为多少元时,才能使日销售利润P取最大值?最大值是多少?