摘要:数学概念的深刻理解并牢固掌握, 其目的是为了能够灵活.正确地运用它, 同时, 在运用的过程中,又能更进一步地深化对数学概念的本质的理解.为此,在教学中应采用多种形式, 引导学生在运算.推理.证明及解决问题的过程中运用数学概念.1.通过反例辩析.及时巩固概念 在中学数学教学中. 很多数学概念(如函数.函数的单调性.奇偶性的定义等)都采用正面阐述的形式.而这些重要概念是解题的基础.若学生对其本质属性含糊不清. 就会在解题过程中混淆.偷换概念. 造成解题失误.为了准确把握概念的本质.可以利用反例来加深对概念的理解.如: 例:下列图形中.不可能是函数的图象是( ) 通过观察.比较.同学们认识到:对于在某个范围内的每一个确定的值.按照某种对应法则.变量都是唯一确定的值和它对应.这才是构成函数关系的本质.所以只能选A. 又如在教学“导数 这一章时.教材中是用割线的极限位置来定义切线的.为此.可以提出以下问题:为什么不说“与曲线只有一个公共点的直线叫做切线 ? 直线与曲线相切, 是否一定只有一个公共点? 对于这两个问题都要通过构造反例进行研究.前一个问题的反例是:抛物线与轴.轴都只有一个公共点, 但只有轴是它的切线, 轴显然不是它的切线,或者与双曲线的渐近线平行的直线与双曲线也只有一个公共点.但它也不是其切线.因此与曲线只有一个公共点的直线不一定是切线.它只符合圆.椭圆等一类曲线.后一个问题也可以举出下列反例.已知曲线C:.可求出曲线C上横坐标为2的点处的切线方程是.但它与曲线C的公共点除了切点外,还有另外一个公共点是(-4.).通过此例可以说明:直线与曲线相切不一定只有一个公共点.当曲线是二次曲线时, 能够保证直线与曲线相切有且只有一个公共点.所以.若能举出恰当的反例加以说明, 会起到正面强调所无法发挥的强化作用, 使概念理解得更加深刻.
网址:http://m.1010jiajiao.com/timu_id_4455054[举报]
我们用符号“||”定义过一些数字概念,如实数绝对值的概念:对于a∈R,|a|=
,可以证明,对任意a,b∈R,不等式|a|-|b|≤|a+b|≤|a|+|b|成立.
(1)再写出两个这类数学概念的定义及其成立的不等式;
(2)对于集合A,定义“|A|”为集合A中元素的个数,对任意的集合A、B有类似的不等式成立吗?如果有,写出一个,并指出等号成立的条件(不必说明理由);如果没有,请说明理由;
(3)设有集合A、B,若|A|=15,|B|≥15,若从A中任取两上元素,恰好都是B中元素的概率p≥
,求|A∩B|的取值范围.
查看习题详情和答案>>
|
(1)再写出两个这类数学概念的定义及其成立的不等式;
(2)对于集合A,定义“|A|”为集合A中元素的个数,对任意的集合A、B有类似的不等式成立吗?如果有,写出一个,并指出等号成立的条件(不必说明理由);如果没有,请说明理由;
(3)设有集合A、B,若|A|=15,|B|≥15,若从A中任取两上元素,恰好都是B中元素的概率p≥
| 1 |
| 5 |
我们用符号“||”定义过一些数字概念,如实数绝对值的概念:对于a∈R,|a|=
,可以证明,对任意a,b∈R,不等式|a|-|b|≤|a+b|≤|a|+|b|成立.
(1)再写出两个这类数学概念的定义及其成立的不等式;
(2)对于集合A,定义“|A|”为集合A中元素的个数,对任意的集合A、B有类似的不等式成立吗?如果有,写出一个,并指出等号成立的条件(不必说明理由);如果没有,请说明理由;
(3)设有集合A、B,若|A|=15,|B|≥15,若从A中任取两上元素,恰好都是B中元素的概率p≥
,求|A∩B|的取值范围.
查看习题详情和答案>>
|
(1)再写出两个这类数学概念的定义及其成立的不等式;
(2)对于集合A,定义“|A|”为集合A中元素的个数,对任意的集合A、B有类似的不等式成立吗?如果有,写出一个,并指出等号成立的条件(不必说明理由);如果没有,请说明理由;
(3)设有集合A、B,若|A|=15,|B|≥15,若从A中任取两上元素,恰好都是B中元素的概率p≥
| 1 |
| 5 |
我们用符号“||”定义过一些数字概念,如实数绝对值的概念:对于a∈R,|a|=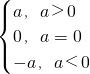 ,可以证明,对任意a,b∈R,不等式|a|-|b|≤|a+b|≤|a|+|b|成立.
,可以证明,对任意a,b∈R,不等式|a|-|b|≤|a+b|≤|a|+|b|成立.
(1)再写出两个这类数学概念的定义及其成立的不等式;
(2)对于集合A,定义“|A|”为集合A中元素的个数,对任意的集合A、B有类似的不等式成立吗?如果有,写出一个,并指出等号成立的条件(不必说明理由);如果没有,请说明理由;
(3)设有集合A、B,若|A|=15,|B|≥15,若从A中任取两上元素,恰好都是B中元素的概率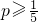 ,求|A∩B|的取值范围.
,求|A∩B|的取值范围.
查看习题详情和答案>>
心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间,上课开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,并趋于稳定.分析结果和实验表明,设提出和讲述概念的时间为x(单位:分),学生的接受能力为f(x)(f(x)值越大,表示接受能力越强),
f(x)=
(1)开讲后多少分钟,学生的接受能力最强?能维持多少时间?
(2)试比较开讲后5分钟、20分钟、35分钟,学生的接受能力的大小;
(3)若一个数学难题,需要56的接受能力以及12分钟时间,老师能否及时在学生一直达到所需接受能力的状态下讲述完这个难题?
查看习题详情和答案>>
f(x)=
|
(1)开讲后多少分钟,学生的接受能力最强?能维持多少时间?
(2)试比较开讲后5分钟、20分钟、35分钟,学生的接受能力的大小;
(3)若一个数学难题,需要56的接受能力以及12分钟时间,老师能否及时在学生一直达到所需接受能力的状态下讲述完这个难题?