摘要:数学概念是多结构.多层次的.理解和掌握数学概念, 应遵循由具体到抽象, 由低级到高级, 由简单到复杂的认知规律.因此, 一个数学概念的建立和形成, 应该通过学生的亲身体验.主动构建, 通过分析.比较.归纳等方式, 揭示出概念的本质属性, 形成完整的概念链, 从而加强学生分析问题, 解决问题的能力, 形成学生的数学思想.可以从以下几方面给予指导.1.分析构成概念的基本要素.数学概念的定义是用精练的数学语言概括表达出来的, 在教学中, 抽象概括出概念后, 还要注意分析概念的定义, 帮助学生认识概念的含义.如为了使学生能更好地掌握函数概念, 我们必须揭示其本质特征, 进行逐层剖析.对定义的内涵要阐明三点:①.的对应变化关系.例如在“函数的表示方法 一节例4的教学.教师要讲明并强调每位同学的“成绩 与“测试时间 之间形成函数关系.使学生明白并非所有的函数都有解析式.由此加深学生对函数的“对应法则 的认识.②实质:每一个值.对应唯一的值.可例举函数讲解:..都是函数.但.的对应关系不同.分别是一对一.二对一.多对一.从而加深对函数本质的认识.再通过图象显示.使学生明白.并非随便一个图形都是函数的图象.从而掌握能成为一个函数图象的图形的条件特征.③定义域.值域.对应法则构成函数的三素.缺一不可.但要特别强调定义域的重要性.由于学生学习解析式较早.比较熟悉.他们往往只关注解析式.忽略定义域而造成错误.为此可让学生比较我函数..的不同并分别求值域.然后结合图象分析得出:三者大相径庭!强调解析式相同但定义域不同的函数决不是相同的函数.再结合分段函数和有实际意义的函数.以引导他们对实际问题的关注和思考.
网址:http://m.1010jiajiao.com/timu_id_4455051[举报]
某商场举行抽奖促销活动,抽奖规则是:从装有6个白球,3个黄球,1个红球的箱子中每次随机地摸出一个球,记下颜色后放回,每人最多摸球三次,摸到红球就中止.摸出一个红球可获得奖金50元,摸出一个黄球可获得奖金20元,摸出白球没有奖金.现设X表示甲在这次抽奖活动中获得的奖金总额.
(1)求P(X>20);
(2)若甲第一次抽得白球,则他在剩下的摸球机会中获得奖金的数学期望是多少?
查看习题详情和答案>>
(1)求P(X>20);
(2)若甲第一次抽得白球,则他在剩下的摸球机会中获得奖金的数学期望是多少?
学数学,其实是要使人聪明,使人的思维更加缜密,在美国广为流传的一道数学题目是:老板给你两个加工资的方案.一是每年年末加一千元;二是每半年结束时加300元.请选择一种.一般不擅长数学的人很容易选择前者,因为一年加一千元总比两个半年共加600元要多.其实,由于工资累计的,时间稍长,往往第二种方案更有利.例如在第二年的年末,依第一种方案可以加得1000+2000=3000元,而第二种方案在第一年加得300+600=900元,第二年加得900+1200=2100元,总数也是900+2100=3000元.但到了第三年,第一种方案可以得到1000+2000+3000=6000元,第二种方案可以得到300+600+900+1200+1500+1800=6300元,比第一方案多了300元.第四年,第五年会更多.因此,你若会在公司干三年以上,则应选择第二种方案.
根据以上材料,解答以下问题:
(1)如果在该公司干10年,问选择第二方案比选择第一方案多加薪多少元?
(2)如果第二方案中得每半年加300元改成每半年加 a元,问 a取何值时,选择第二方案总是比选择第一方案多加薪? 查看习题详情和答案>>
根据以上材料,解答以下问题:
(1)如果在该公司干10年,问选择第二方案比选择第一方案多加薪多少元?
(2)如果第二方案中得每半年加300元改成每半年加 a元,问 a取何值时,选择第二方案总是比选择第一方案多加薪? 查看习题详情和答案>>
在美国广为流传的一道数学题目是:老板给你两种加工资的方案.第一种方案是每年年末(12月底)加薪一次,每次所加的工资数是在上次所加工资数的基础上再增加1000元;第二种方案是每半年(6月底和12月底)各加薪一次,每次所加的工资数是在上次所加工资数的基础上再增加300元,请选择一种.
根据上述条件,试问:
(1)如果你将在该公司干十年,你将选择哪一种加工资的方案?(说明理由)
(2)如果第二种方案中的每半年加300元改成每半年加a元,那么a在什么范围内取值时,选择第二种方案总是比选择第一种方案多加薪? 查看习题详情和答案>>
根据上述条件,试问:
(1)如果你将在该公司干十年,你将选择哪一种加工资的方案?(说明理由)
(2)如果第二种方案中的每半年加300元改成每半年加a元,那么a在什么范围内取值时,选择第二种方案总是比选择第一种方案多加薪? 查看习题详情和答案>>
体育课的排球发球项目考试的规则是: 每位学生最多可发球3次,一旦发球成功,则停止发球,否则一直发到3次为止. 设学生一次发球成功的概率为p (p ¹ 0),发球次数为X,若X的数学期望EX >1.75,则p的取值范围是 ( )
A. (0,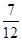 ) B. (
) B. (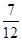 ,1) C. (0,
,1) C. (0, ) D. (
) D. ( ,1)
,1)
查看习题详情和答案>>
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分)
在美国广为流传的一道数学题目是:老板给你两种加工资的方案。第一种方案是每年年末(12月底)加薪一次,每次所加的工资数是在上次所加工资数的基础上再增加1000元;第二种方案是每半年(6月底和12月底)各加薪一次,每次所加的工资数是在上次所加工资数的基础上再增加300元,请选择一种.
根据上述条件,试问:
(1)如果你将在该公司干十年,你将选择哪一种加工资的方案?(说明理由)
(2)如果第二种方案中的每半年加300元改成每半年加a元,那么a在什么范围内取值时,选择第二种方案总是比选择第一种方案多加薪?
查看习题详情和答案>>