摘要：19．解:当n=1时.由(n-1)an+1=(n+1)(an-1),得a1=1. 当n=2时.a2=6代入得a3=15.同理a4=28,再代入bn=an+n,有b1=2,b2=8,b3=18,b4=32,---.由此猜想bn=2n2. 要证bn=2n2,只需证an=2n2-n. ①当n=1时.a1=2×12-1=1成立. ②假设当n=k时.ak=2k2-k成立. 那么当n=k+1时.由(k-1)ak+1=(k+1)(ak-1),得a k+1=(ak-1) =(2k2-k-1)=(2k+1)(k-1)=(k+1)(2k+1)=2(k+1)2-(k+1). ∴当n=k+1时.an=2n2-n正确.从而bn=2n2.
网址：http://m.1010jiajiao.com/timu_id_4453412[举报]
设二次函数f(x)＝(k－4)x2＋kx(k∈R)，对任意实数x，有f(x)≤6x＋2恒成立；数列{an}满足an+1＝f(an)．
(1)求函数f(x)的解析式；
(2)试写出一个区间(a，b)，使得当an∈(a，b)时，an+1∈(a，b)且数列{an}是递增数列，并说明理由；
(3)已知a1＝
，是否存在非零整数λ，使得对任意n∈N*，都有
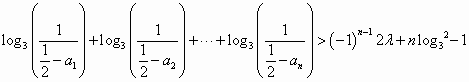－1＋(－1)n－12λ＋nlog32恒成立，若存在，求之；若不存在，说明理由．
| |||||||||||
；②当n≥2时，从A口输入n，从B口得的结果an是将前一结果an－1先乘以自然数列{n}中的第n－1个奇数，再除以自然数列{n}中的第n＋1个奇数，试问：