摘要: 中.求的最小值. [答案]
网址:http://m.1010jiajiao.com/timu_id_4453226[举报]
如图,在四棱柱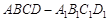 中,侧棱
中,侧棱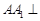 底面
底面 ,
,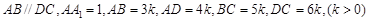
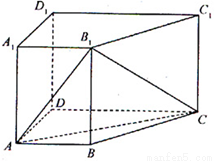
(Ⅰ)求证: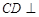 平面
平面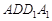
(Ⅱ)若直线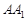 与平面
与平面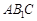 所成角的正弦值为
所成角的正弦值为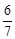 ,求
,求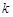 的值
的值
(Ⅲ)现将与四棱柱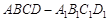 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为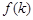 ,写出
,写出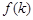 的解析式。(直接写出答案,不必说明理由)
的解析式。(直接写出答案,不必说明理由)
查看习题详情和答案>>
如图,在四棱柱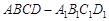 中,侧棱
中,侧棱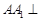 底面
底面 ,
,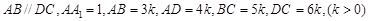
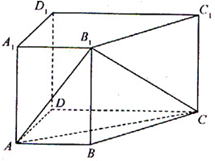
(Ⅰ)求证: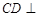 平面
平面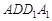
(Ⅱ)若直线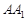 与平面
与平面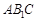 所成角的正弦值为
所成角的正弦值为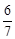 ,求
,求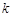 的值
的值
(Ⅲ)现将与四棱柱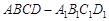 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为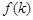 ,写出
,写出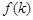 的解析式。(直接写出答案,不必说明理由)
的解析式。(直接写出答案,不必说明理由)
如图,在四棱柱 中,侧棱
中,侧棱 底面
底面 ,
,

(Ⅰ)求证: 平面
平面
(Ⅱ)若直线 与平面
与平面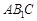 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值
的值
(Ⅲ)现将与四棱柱 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为 ,写出
,写出 的解析式。(直接写出答案,不必说明理由)
的解析式。(直接写出答案,不必说明理由)
 中,侧棱
中,侧棱 底面
底面 ,
,

(Ⅰ)求证:
 平面
平面
(Ⅱ)若直线
 与平面
与平面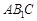 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值
的值(Ⅲ)现将与四棱柱
 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为 ,写出
,写出 的解析式。(直接写出答案,不必说明理由)
的解析式。(直接写出答案,不必说明理由)一次数学考试共有10道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的,设计试卷时,安排前n道题使考生都能得出正确答案,安排8-n道题,每题得出正确答案的概率为 ,安排最后两道题,每题得出正确答案的概率为
,安排最后两道题,每题得出正确答案的概率为 ,且每题答对与否相互独立,同时规定:每题选对得5分,不选或选错得0分。
,且每题答对与否相互独立,同时规定:每题选对得5分,不选或选错得0分。
(1)当n=6时,
①分别求考生10道题全答对的概率和答对8道题的概率;
②问考生答对几道题的概率最大,并求出最大值;
(2)要使考生所得分数的期望不小于40分,求n的最小值。
查看习题详情和答案>>
 ,安排最后两道题,每题得出正确答案的概率为
,安排最后两道题,每题得出正确答案的概率为 ,且每题答对与否相互独立,同时规定:每题选对得5分,不选或选错得0分。
,且每题答对与否相互独立,同时规定:每题选对得5分,不选或选错得0分。(1)当n=6时,
①分别求考生10道题全答对的概率和答对8道题的概率;
②问考生答对几道题的概率最大,并求出最大值;
(2)要使考生所得分数的期望不小于40分,求n的最小值。
请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
| |||
| |||
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,满分60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数![]() 的定义域为
的定义域为![]() ,
,![]() 的定义域为
的定义域为![]() ,则
,则![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 空集
空集
2.已知复数![]() ,则它的共轭复数等于
,则它的共轭复数等于
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3.设变量![]() 、
、![]() 满足线性约束条件
满足线性约束条件 ,则目标函数
,则目标函数![]() 的最小值为
的最小值为
![]() 6
6 ![]() 7
7 ![]() 8
8 ![]() 23
23