若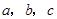是不全相等的实数，求证：．

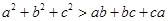证明过程如下：

，，，，

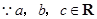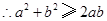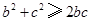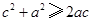又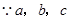不全相等，

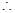以上三式至少有一个“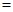”不成立，

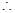将以上三式相加得，

．

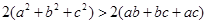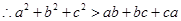此证法是（    ）

A．分析法       B．综合法       C．分析法与综合法并用       D．反证法

若a，b，c是不全相等的实数，求证：a²＋b²＋c²>ab＋bc＋ca.

证明过程如下：

∵a、b、c∈R，∴a²＋b²≥2ab，

b²＋c²≥2bc，c²＋a²≥2ac，

又∵a，b，c不全相等，

∴以上三式至少有一个“＝”不成立，

∴将以上三式相加得2(a²＋b²＋c²)>2(ab＋bc＋ac)，

∴a²＋b²＋c²>ab＋bc＋ca.

此证法是(　　)

(A)分析法                      (B)综合法

(C)分析法与综合法并用      (D)反证法

老师给出一个函数，四个学生甲、乙、丙、丁各指出这个函数的一个性质：
甲：对于任意x∈R，都有f（1+x）=f（1-x）；
乙：在（-∞，0]上，函数f(x)单调递减；
丙：在（0，+∞）上，函数f(x)单调递增；
丁：f（0）不是函数f(x)的最小值。
如果其中有三个人说得正确，则这个函数f(x)的解析式可能是_______。

老师给出一个函数，四个学生甲、乙、丙、丁各指出这个函数的一个性质：

甲：对于任意x∈R，都有f（1+x）=f（1-x）；

乙：在（-∞，0]上，函数f(x)单调递减；

丙：在（0，+∞）上，函数f(x)单调递增；

丁：f（0）不是函数f(x)的最小值。

如果其中有三个人说得正确，则这个函数f(x)的解析式可能是_______。

设椭圆（常数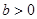）的左右焦点分别为，是直线上的两个动点，．

（1）若，求的值；

（2）求的最小值．

【解析】第一问中解：设，则

由得    由，得

  ② 

第二问易求椭圆的标准方程为：

，

所以，当且仅当或时，取最小值．

解：设， ……………………1分

则，由得     ①……2分

（1）由，得  ②   ……………1分

    ③    ………………………1分

由①、②、③三式，消去，并求得． ………………………3分

（2）解法一：易求椭圆的标准方程为：．………………2分

， ……4分

所以，当且仅当或时，取最小值．…2分

解法二：， ………………4分

所以，当且仅当或时，取最小值