摘要:换元法:换元法是数学中一个非常重要而且应用十分广泛的解题方法.我们通常把未知数或变数称为元.所谓换元法.就是在一个比较复杂的数学式子中.用新的变元去代替原式的一个部分或改造原来的式子.使它简化.使问题易于解决.
网址:http://m.1010jiajiao.com/timu_id_4449630[举报]
换元法是把一个比较复杂的数学式子的一部分看成是一个整体,用另一个字母代替这一部分(即换元).换元法的好处是能使式子得到简化,各项的关系容易看清,便于解决问题.此方法充分体现了整体的数学思想.例如:用换元法解分式方程
-
=2时,如果设
=y,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成
=y1和
=y2,即可解出x1和x2.请用换元法解方程:x2-
=2x-1.
查看习题详情和答案>>
| 2x-1 |
| x |
| x |
| 2x-1 |
| 2x-1 |
| x |
| 2x-1 |
| x |
| 2x-1 |
| x |
| 12 |
| x2-2x |
换元法是把一个比较复杂的数学式子的一部分看成是一个整体,用另一个字母代替这一部分(即换元).换元法的好处是能使式子得到简化,各项的关系容易看清,便于解决问题.此方法充分体现了整体的数学思想.例如:用换元法解分式方程 时,如果设
时,如果设 ,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成
,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成 和
和 ,即可解出x1和x2.请用换元法解方程:
,即可解出x1和x2.请用换元法解方程: .
.
查看习题详情和答案>>
 时,如果设
时,如果设 ,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成
,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成 和
和 ,即可解出x1和x2.请用换元法解方程:
,即可解出x1和x2.请用换元法解方程: .
.查看习题详情和答案>>
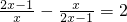 时,如果设
时,如果设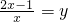 ,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成
,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成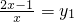 和
和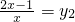 ,即可解出x1和x2.请用换元法解方程:
,即可解出x1和x2.请用换元法解方程: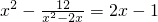 .
.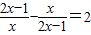 时,如果设
时,如果设 ,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成
,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成 和
和 ,即可解出x1和x2.请用换元法解方程:
,即可解出x1和x2.请用换元法解方程: .
.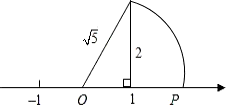 “数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是
“数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是 ”,这种利用图形直观说明问题的方式体现的数学思想方法叫
”,这种利用图形直观说明问题的方式体现的数学思想方法叫