摘要：1471年.德国数学家米勒提出了雕塑问题:假定有一个雕塑高AB=3米.立在一个底座上.底座的高BC=2.2米.一个人注视着这个雕塑并朝它走去.这个人的水平视线离地1.7米.问此人应站在离雕塑底座多远处.才能使看雕塑的效果最好.所谓看雕塑的效果最好是指看雕塑的视角最大.问题转化为在水平视线EF上求使视角最大的点.如图:过A.B两点.作一圆与EF相切于点M.你能说明点M为所求的点吗?并求出此时这 个人离雕塑底座的距离?
网址：http://m.1010jiajiao.com/timu_id_4449625[举报]
计算（本题满分12分，每题4分）
(1) ―12012+ (
)－1―(3.14－π)0
（2） (－6xy2)2(―
xy + y2―x2)
(3) 先化简，再求值：(2m+n)2－(3m－n)2+5m(m－n)，其中m=
，n=
．
查看习题详情和答案>>
(本题满分8分)
如图，在
中，
，
，BC=6．
是AB边上的一个动点(异于
、
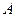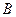两点)，过点分别作
、
边的垂线，垂足为
、
．设
．
(1)在中，
=" " ▲ ；
(2)当
=" " ▲ 时，矩形
的周长是14；
(3)是否存在的值，使得
的面积、
的面积与矩形的面积同时相等?请说出你的判断，并加以说明．
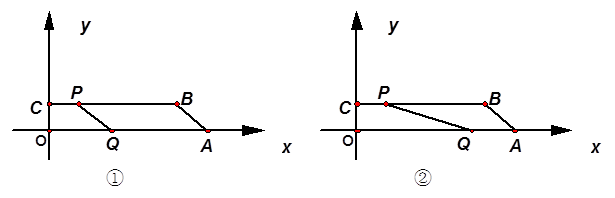
．(本题满分12分) 如图，在平面直角坐标系中，四边形OABC为直角梯形，OA∥BC，BC=14，A（16，0），C（0，2）.
1.(1)如图①，若点P、Q分别从点C、A同时出发，点P以每秒2个单位的速度由C向B运动，点Q以每秒4个单位的速度由A向O运动，当点Q停止运动时，点P也停止运动.设运动时间为t秒（0≤t≤4）.
①求当t为多少时，四边形PQAB为平行四边形？(4分)
②求当t为多少时，直线PQ将梯形OABC分成左右两部分的比为1:2，并求出此时直线PQ的解析式. (4分)
2.（2）如图②，若点P、Q分别是线段BC、AO上的任意两点（不与线段BC、AO的端点重合），且四边形OQPC面积为10，试说明直线PQ一定经过一定点，并求出该定点的坐标. (4分)
