摘要: 解:(Ⅰ)∵f(x)的定义域D= ∴数列{xn}只有三项x1=.x2=.x3=-1 (Ⅱ)∵f(x)==x即x2-3x+2=0.∴x=1或x=2 即x0=1或2时.xn+1==xn 故当x0=1时.x0=1,当x0=2时.xn=2(n∈N) (Ⅲ)解不等式x<.得x<-1或1<x<2. 要使x1<x2.则x2<-1或1<x1<2 对于函数f(x)= 若x1<-1.则x2=f(x1)>4.x3=f(x2)<x2 当1<x1<2时.x2=f(x)>x1且1<x2<2 依次类推可得数列{xn}的所有项均满足xn+1>xn(n∈N) 综上所述.x1∈(1.2).由x1=f(x0).得x0∈(1.2) 第二讲 结构图 [知识梳理] [知识盘点]
网址:http://m.1010jiajiao.com/timu_id_4447386[举报]
(普通班)函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
A.(-1,1) B.(-1,+∞) C.(-∞,-1) D.(-∞,+∞)
(实验班)已知可导函数 的导函数为
的导函数为 ,且满足:①
,且满足:① ,②
,② ,记
,记 ,
, ,
, ,则
,则 的大小顺序为( )
的大小顺序为( )
A.
 B.
B.
 C.
C.
 D.
D.

查看习题详情和答案>>
(普通班)函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
A.(-1,1) B.(-1,+∞) C.(-∞,-1) D.(-∞,+∞)
(实验班)已知可导函数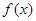 的导函数为
的导函数为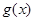 ,且满足:①
,且满足:①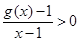 ,②
,②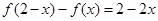 ,记
,记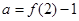 ,
,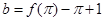 ,
,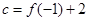 ,则
,则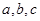 的大小顺序为( )
的大小顺序为( )
A.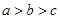 B.
B. 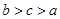 C.
C. 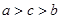 D.
D. 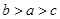
A.(-1,1) B.(-1,+∞) C.(-∞,-1) D.(-∞,+∞)
(实验班)已知可导函数
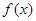 的导函数为
的导函数为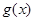 ,且满足:①
,且满足:①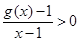 ,②
,②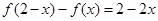 ,记
,记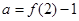 ,
,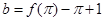 ,
,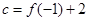 ,则
,则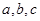 的大小顺序为( )
的大小顺序为( )A.
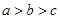 B.
B. 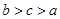 C.
C. 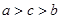 D.
D. 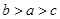
已知函数f(x)的定义域为D,且f(x)同时满足以下条件:
①f(x)在D上单调递增或单调递减;
②存在区间[a,b] D,使得f(x)在[a,b]上的值域是[a,b],那么我们把函数f(x)(x∈D)叫做闭函数.
D,使得f(x)在[a,b]上的值域是[a,b],那么我们把函数f(x)(x∈D)叫做闭函数.
(1)求闭函数y=-x3符合条件2的区间[a,b].
(2)判断函数y=2x-lgx是不是闭函数?若是,请说明理由,并找出区间[a,b];若不是,请说明理由.
(3)若y=k+ 是闭函数,求实数k的取值范围.
是闭函数,求实数k的取值范围.

