摘要:如图.在平面直角坐标系中.已知矩形ABCD的三个顶点B(4.0).C(8.0).D(8.8).抛物线y=ax2+bx过A.C两点. (1)直接写出点A的坐标.并求出抛物线的解析式, (2)动点P从点A出发.沿线段AB向终点B运动.同时点Q从点C出发.沿线段CD 向终点D运动.速度均为每秒1个单位长度.运动时间为t秒.过点P作PE⊥AB交AC于点E ①过点E作EF⊥AD于点F.交抛物线于点G.当t为何值时.线段EG最长? ②连接EQ.在点P.Q运动的过程中.判断有几个时刻使得△CEQ是等腰三角形? 请直接写出相应的t值. 解.(1)点A的坐标为(4.8) -------1分 将A 两点坐标分别代入y=ax2+bx 8=16a+4b 得 0=64a+8b 解 得a=-,b=4 ∴抛物线的解析式为:y=-x2+4x -------3分 (2)①在Rt△APE和Rt△ABC中.tan∠PAE==,即= ∴PE=AP=t.PB=8-t. ∴点E的坐标为(4+t.8-t). ∴点G的纵坐标为:-(4+t)2+4(4+t)=-t2+8. -------5分 ∴EG=-t2+8-(8-t) =-t2+t. ∵-<0.∴当t=4时.线段EG最长为2. -------7分 ②共有三个时刻. -------8分 t1=. t2=.t3= . -------11分
网址:http://m.1010jiajiao.com/timu_id_4444536[举报]
 解答下列问题:
解答下列问题: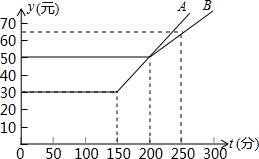 009年1月通话时间相同,费用差额为10元.请你确定小明2009年1月的通话时间.
009年1月通话时间相同,费用差额为10元.请你确定小明2009年1月的通话时间.