摘要:1.定义: ⑴等差数列 , ⑵等比数列 ,
网址:http://m.1010jiajiao.com/timu_id_4443471[举报]
等差数列与等比数列之间是存在某种结构的类比关系的,例如从定义看,或者从通项公式看,都可以发现这种类比的原则.按照此思想,请把下面等差数列的性质,类比到等比数列,写出相应的性质:若{an}为等差数列,am=a,an=b(m<n),则公差d=
;若{bn}是各项均为正数的等比数列,bm=a,bn=b(m<n),则公比q=
.
查看习题详情和答案>>
| b-a |
| n-m |
| n-m |
| ||
| n-m |
| ||
等差数列与等比数列之间是存在某种结构的类比关系的,例如从定义看,或者从通项公式看,都可以发现这种类比的原则.按照此思想,请把下面等差数列的性质,类比到等比数列,写出相应的性质:若{an}为等差数列,am=a,an=b(m<n),则公差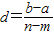 ;若{bn}是各项均为正数的等比数列,bm=a,bn=b(m<n),则公比q= .
查看习题详情和答案>>
;若{bn}是各项均为正数的等比数列,bm=a,bn=b(m<n),则公比q= .
查看习题详情和答案>>
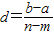 ;若{bn}是各项均为正数的等比数列,bm=a,bn=b(m<n),则公比q= .
查看习题详情和答案>>
;若{bn}是各项均为正数的等比数列,bm=a,bn=b(m<n),则公比q= .
查看习题详情和答案>>
定义:若一个数列中的每一项都是另一个数列中的项,则称这个数列是另一个数列的子数列。已知![]() 是等差数列,
是等差数列,![]() 是公比为
是公比为![]() 的等比数列,
的等比数列,![]() ,
,![]() ,记
,记![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(Ⅰ)若![]() (
(![]() 是大于
是大于![]() 的正整数),求证:
的正整数),求证:![]() ;
;
(Ⅱ)若![]() (
(![]() 是某个正整数),求证:
是某个正整数),求证:![]() 是整数,且数列
是整数,且数列![]() 是数列
是数列![]() 的子数列.
的子数列.