3．直线与圆锥曲线问题解法: ⑴直接法:联立直线与圆锥曲线方程.构造一元二次方程求解. 注意以下问题:①联立的关于“ 还是关于“ 的一元二次方程? ②直线斜率不存在时考虑了吗?③判别式验证了吗?——青夏教育精英家教网——

摘要：3．直线与圆锥曲线问题解法: ⑴直接法:联立直线与圆锥曲线方程.构造一元二次方程求解. 注意以下问题:①联立的关于“ 还是关于“ 的一元二次方程? ②直线斜率不存在时考虑了吗?③判别式验证了吗? ⑵设而不求:--------处理弦中点问题步骤如下:①设点A(x1.y1).B(x2,y2),②作差得,③解决问题.

网址：http://m.1010jiajiao.com/timu_id_4443468[举报]

已知圆锥曲线C上任意一点到两定点F₁（-1，0）、F₂（1，0）的距离之和为常数，曲线C的离心率e=

．
（1）求圆锥曲线C的方程；
（2）设经过点F₂的任意一条直线与圆锥曲线C相交于A、B，试证明在x轴上存在一个定点P，使

的值是常数．查看习题详情和答案>>

下列是有关直线与圆锥曲线的命题：
①过点（2，4）作直线与抛物线y²=8x有且只有一个公共点，这样的直线有2条；
②过抛物线y²=4x的焦点作一条直线与抛物线相交于A，B两点，它们的横坐标之和等于5，则这样的直线有且仅有两条；
③过点（3，1）作直线与双曲线

-y2=1有且只有一个公共点，这样的直线有3条；
④过双曲线x2-

=1的右焦点作直线l交双曲线于A，B两点，若|AB|=4，则满足条件的直线l有3条；
⑤已知双曲线x2-

=1和点A（1，1），过点A能作一条直线l，使它与双曲线交于P，Q两点，且点A恰为线段PQ的中点．
其中说法正确的序号有

．（请写出所有正确的序号）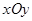

查看习题详情和答案>>

11、教材中“坐标平面上的直线”与“圆锥曲线”两章内容体现出解析几何的本质是

用代数的方法研究图形的几何性质

查看习题详情和答案>>

教材中“坐标平面上的直线”与“圆锥曲线”两章内容体现出解析几何的本质是．查看习题详情和答案>>

（本小题满分10分）选修4-4：坐标系与参数方程

已知在直角坐标系中，圆锥曲线的参数方程为（为参数），定点，是圆锥曲线的左，右焦点．

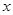（Ⅰ）以原点为极点、轴正半轴为极轴建立极坐标系，求经过点且平行于直线的直线的极坐标方程；[来源:ZXXK]

（Ⅱ）在（I）的条件下，设直线与圆锥曲线交于两点，求弦的长．

查看习题详情和答案>>