摘要:例1解关于x的不等式 分析 此不等式为含参数k的不等式.当k值不同时相应的二次方程的判别式的值也不同.故应先从讨论判别式入手. 解 (1) 当有两个不相等的实根. 所以不等式: (2) 当有两个相等的实根. 所以不等式.即, (3) 当无实根 所以不等式解集为. 说明 一元二次方程.一元二次不等式.一元二次函数有着密切的联系.要注意数形结合研究问题. 小结:讨论.即讨论方程根的情况 例2.解关于x的不等式:(x-+12)(x+a)<0. 解:①将二次项系数化“+ 为:(-x-12)(x+a)>0. ②相应方程的根为:-3.4.-a.现a的位置不定.应如何解? ③讨论: ⅰ当-a>4.即a<-4时.各根在数轴上的分布及穿线如下: ∴原不等式的解集为{x| -3<x<4或x>-a}. ⅱ当-3<-a<4.即-4<a<3时.各根在数轴上的分布及穿线如下: ∴原不等式的解集为{x| -3<x<-a或x>4}. ⅲ当-a<-3.即a>3时.各根在数轴上的分布及穿线如下: ∴原不等式的解集为{x| -a<x<-3或x>4}. ⅳ0当-a=4.即a=-4时.各根在数轴上的分布及穿线如下: ∴原不等式的解集为{x| x>-3}. ⅴ当-a=-3.即a=3时.各根在数轴上的分布及穿线如下: ∴原不等式的解集为{x| x>4}. 小结:讨论方程根之间的大小情况 例3若不等式对于x取任何实数均成立.求k的取值范围. 解:∵ . ∴原不等式对x取任何实数均成立.等价于不等式2x2-2(k-3)x+3-k>0对x取任何实数均成立. ∴=[-2<0k2-4k+3<01<k<3. ∴k的取值范围是(1.3). 小结:逆向思维题目.告诉解集反求参数范围.即确定原不等式.待定系数法的一部分 例4 已知关于x的二次不等式:a+(a-1)x+a-1<0的解集为R.求a的取值范围. 分析:原不等式的解集为R.即对一切实数x不等式都成立.故必然y= a+(a-1)x+a-1的图象开口向下.且与x轴无交点.反映在数量关系上则有a<0 且<0. 解:由题意知.要使原不等式的解集为R.必须. 即 a<-. ∴a的取值范围是a∈(-,-). 说明:本题若无“二次不等式 的条件.还应考虑a=0的情况.但对本题讲a=0时式子不恒成立. 练习:已知(-1) -(a-1)x-1<0的解集为R.求实数a的取值范围. 解:若-1=0.即a=1或a=-1时.原不等式的解集为R和{x|x<}, 若-10.即a1时.要使原不等式的解集为R. 必须. ∴实数a的取值范围是(-,1)∪{1}=(-,1).
网址:http://m.1010jiajiao.com/timu_id_4441846[举报]
 的不等式
的不等式

 ;
; 
 时,原不等式的解集为
时,原不等式的解集为 ;
; 时,原不等式的解集为
时,原不等式的解集为 ;
; 时,原不等式的解集为
时,原不等式的解集为 。
。 
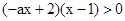
 原不等式的解集为
原不等式的解集为 。
。 的两个焦点分别为
的两个焦点分别为 、
、 ,离心率为2.
,离心率为2. 能否作出直线
能否作出直线 ,使
,使 交于
交于 、
、 两点,且
两点,且 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由. ,然后直线方程与双曲线方程联立,消去y,得到关于x的一元二次方程,利用韦达定理
,然后直线方程与双曲线方程联立,消去y,得到关于x的一元二次方程,利用韦达定理