摘要:22.A选修4-1:几何证明选讲 如图.已知是的切线.为切点.是的割线.与交于两点.圆心在的内部.点是的中点. (Ⅰ)证明四点共圆, (Ⅱ)求的大小. (Ⅰ)证明:连结. 因为与相切于点.所以. 因为是的弦的中点.所以. 于是. 由圆心在的内部.可知四边形的对角互补.所以四点共圆. 得四点共圆.所以. 由(Ⅰ)得. 由圆心在的内部.可知. 所以
网址:http://m.1010jiajiao.com/timu_id_4441062[举报]
(本小题满分10分).选修4-1:几何证明选讲
在 中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。

(1)求证:  ;(5分)
;(5分)
(2)若AC=3,求 的值。(5分)
的值。(5分)
查看习题详情和答案>>
(本小题满分10分)选修4-1:几何证明选讲
如图,锐角△ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为内切圆I与边CA的切点.
(Ⅰ)求证:四点A,I,H,E共圆;
(Ⅱ)若∠C=50°,求∠IEH的度数.

查看习题详情和答案>>
(本小题满分10分)选修4-1:几何证明选讲
如图,锐角△ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为内切圆I与边CA的切点.
(Ⅰ)求证:四点A,I,H,E共圆;
(Ⅱ)若∠C=50°,求∠IEH的度数.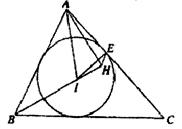
如图,锐角△ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为内切圆I与边CA的切点.
(Ⅰ)求证:四点A,I,H,E共圆;
(Ⅱ)若∠C=50°,求∠IEH的度数.

 ;
;
 ABC中,AB=AC,
D是
ABC中,AB=AC,
D是  CDE;
CDE; ,求
,求