摘要:在ABC中 ⑴如图1.若P点是∠ABC和∠ACB的角平分线的交点.则∠P=90°∠A, ⑵如图2.若P点是∠ABC和外角∠ACE的角平分线的交点.则∠P=90°-∠A, ⑶如图3.若P点是外角∠CBF和∠BCE的角平分线的交点.则∠P=90°-∠A. 上述说法下确的个数是( ). A.0个 B.1个 C.2个 D.3个
网址:http://m.1010jiajiao.com/timu_id_4439040[举报]
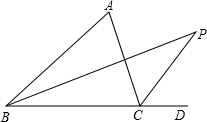 如图,在△ABC中,内角平分线BP和外角平分线CP相交于点P,根据下列条件求∠P的度数.
如图,在△ABC中,内角平分线BP和外角平分线CP相交于点P,根据下列条件求∠P的度数.(1)若∠ABC=50°,∠ACB=80°,则∠P=
25°
25°
,若∠ABC+∠ACB=110°,则∠P=35°
35°
;(2)若∠BAC=90°,则∠P=
45°
45°
;(3)从以上的计算中,你能发现∠P与∠BAC的关系是
∠P=
∠A
| 1 |
| 2 |
∠P=
∠A
;| 1 |
| 2 |
(4)证明第(3)题中你所猜想的结论.
 如图,在△ABC中,内角平分线BP和外角平分线CP相交于点P,根据下列条件求∠P的度数.
如图,在△ABC中,内角平分线BP和外角平分线CP相交于点P,根据下列条件求∠P的度数.
(1)若∠ABC=50°,∠ACB=80°,则∠P=______,若∠ABC+∠ACB=110°,则∠P=______;
(2)若∠BAC=90°,则∠P=______;
(3)从以上的计算中,你能发现∠P与∠BAC的关系是______;
(4)证明第(3)题中你所猜想的结论.
查看习题详情和答案>>
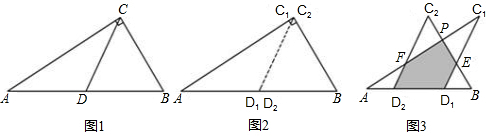
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC1D1和△BC2D2两个三角形(如图所示).将纸片△AC1D1沿直线D2B(AB)方向平移(点A,D1,D2,B始终在同一直线上),当点D1于点B重合时,停止平移.在平移过程中,C1D1与BC2交于点E,AC1与C2D2、BC2分别交于点F、P.
(1)当△AC1D1平移到如图3所示的位置时,猜想图中的D1E与D2F的数量关系,并证明你的猜想;
(2)设平移距离D2D1为x,△AC1D1与△BC2D2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=
S△ABC;若不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)当△AC1D1平移到如图3所示的位置时,猜想图中的D1E与D2F的数量关系,并证明你的猜想;
(2)设平移距离D2D1为x,△AC1D1与△BC2D2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=
| 1 | 4 |
 查看习题详情和答案>>
查看习题详情和答案>>
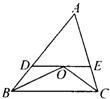 6、如图,在△ABC中,∠ABC和∠ACB的角平分线交于点O,DE∥BC,若AB=8,AC=6,则△ADE的周长是( )
6、如图,在△ABC中,∠ABC和∠ACB的角平分线交于点O,DE∥BC,若AB=8,AC=6,则△ADE的周长是( ) 如图,在△ABC中,∠ABC和∠ACB的角平分线交于点O,DE∥BC,若AB=8,AC=6,则△ADE的周长是
如图,在△ABC中,∠ABC和∠ACB的角平分线交于点O,DE∥BC,若AB=8,AC=6,则△ADE的周长是