摘要：直线的方程是指( ) A.直线上点的坐标都是方程的解 B.以方程的解为坐标的点都在直线上 C.直线上点的坐标都是方程的解.且以方程的解为坐标的点都在直线上 D.以上都不对
网址：http://m.1010jiajiao.com/timu_id_4436230[举报]
设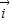
、
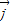为直角坐标平面内x、y轴正方向上的单位向量，若向量
，
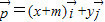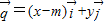，（x，y∈R，m≥2），且
．
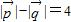（1）求动点M（x，y）的轨迹方程？并指出方程所表示的曲线；
（2）已知点A（0，1}，设直线l：y=
x-3与点M的轨迹交于B、C两点，问是否存在实数m，使得
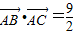？若存在，求出m的值；若不存在，说明理由．
查看习题详情和答案>>
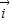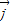、为直角坐标平面内x、y轴正方向上的单位向量，若向量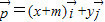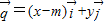，，（x，y∈R，m≥2），且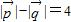．（1）求动点M（x，y）的轨迹方程？并指出方程所表示的曲线；
（2）已知点A（0，1}，设直线l：y=
x-3与点M的轨迹交于B、C两点，问是否存在实数m，使得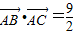？若存在，求出m的值；若不存在，说明理由．查看习题详情和答案>>
已知点
是直角坐标平面内的动点，点到直线
的距离为
，到点
的距离为
，且
．
(1)求动点P所在曲线C的方程；
(2)直线
过点F且与曲线C交于不同两点A、B(点A或B不在x轴上)，分别过A、B点作直线
的垂线，对应的垂足分别为
，试判断点F与以线段
为直径的圆的位置关系(指在圆内、圆上、圆外等情况)；
(3)记
，
，
(A、B、
是(2)中的点)，问是否存在实数
，使
成立．若存在，求出的值；若不存在，请说明理由．
进一步思考问题：若上述问题中直线
、点
、曲线C：
，则使等式成立的的值仍保持不变．请给出你的判断 (填写“不正确”或“正确”)(限于时间，这里不需要举反例，或证明)．
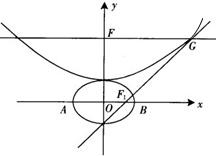设b＞0，椭圆方程为| x2 |
| 2b2 |
| y2 |
| b2 |
| 1 |
| 8 |
（1）求点G和点F1的坐标（用b表示）；
（2）求满足条件的椭圆方程和抛物线方程；
（3）设A，B分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在点P，使得△ABP为直角三角形？若存在，指出共有几个这样的点？并说明理由（不必具体求出这些点的坐标）． 查看习题详情和答案>>
已知点P是直角坐标平面内的动点，点P到直线l1：x=-2的距离为d1，到点F（-1，0）的距离为d2，且
=
．
（1）求动点P所在曲线C的方程；
（2）直线l过点F且与曲线C交于不同两点A、B（点A或B不在x轴上），分别过A、B点作直线l1：x=-2的垂线，对应的垂足分别为M、N，试判断点F与以线段MN为直径的圆的位置关系（指在圆内、圆上、圆外等情况）；
（3）记S1=S△FAM，S2=S△FMN，S3=S△FBN（A、B、M、N是（2）中的点），问是否存在实数λ，使S22=λS1S3成立．若存在，求出λ的值；若不存在，请说明理由．
进一步思考问题：若上述问题中直线l1：x=-
、点F（-c，0）、曲线C：
+
=1(a＞b＞0，c=
)，则使等式S22=λS1S3成立的λ的值仍保持不变．请给出你的判断 （填写“不正确”或“正确”）（限于时间，这里不需要举反例，或证明）．
查看习题详情和答案>>
| d2 |
| d1 |
| ||
| 2 |
（1）求动点P所在曲线C的方程；
（2）直线l过点F且与曲线C交于不同两点A、B（点A或B不在x轴上），分别过A、B点作直线l1：x=-2的垂线，对应的垂足分别为M、N，试判断点F与以线段MN为直径的圆的位置关系（指在圆内、圆上、圆外等情况）；
（3）记S1=S△FAM，S2=S△FMN，S3=S△FBN（A、B、M、N是（2）中的点），问是否存在实数λ，使S22=λS1S3成立．若存在，求出λ的值；若不存在，请说明理由．
进一步思考问题：若上述问题中直线l1：x=-
| a2 |
| c |
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
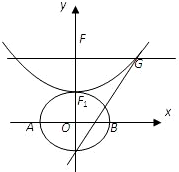设b＞0，椭圆方程为