摘要:向量在空间中的应用.在空间坐标系下.通过向量的坐标的表示.运用计算的方法研究三维空间几何图形的性质. 在复习过程中.抓住源于课本.高于课本的指导方针.本章考题大多数是课本的变式题.即源于课本.因此.掌握双基.精通课本是本章关键.
网址:http://m.1010jiajiao.com/timu_id_4435250[举报]
在平面直角坐标系中,对其中任何一向量X=(x1,x2),定义范数||X||,它满足以下性质:(1)||X||≥0,当且仅当X为零向量时,不等式取等号;(2)对任意的实数λ,||λX||=|λ|•||X||(注:此处点乘号为普通的乘号);(3)||X||+||Y||≥||X+Y||.应用类比的方法,我们可以给出空间直角坐标系下范数的定义,现有空间向量X=(x1,x2,x3),下面给出的几个表达式中,可能表示向量X的范数的是 (把所有正确答案的序号都填上)
(1)
+2x22+x32(2)
(3)
(4)
.
查看习题详情和答案>>
(1)
| x12 |
| 2x2-x22+x32 |
| x12+x22+x32+2 |
| x12+x22+x32 |
 在边长是2的正方体ABCD-A1B1C1D1中,E,F分别为AB,A1C的中点.应用空间向量方法求解下列问题.
在边长是2的正方体ABCD-A1B1C1D1中,E,F分别为AB,A1C的中点.应用空间向量方法求解下列问题.(1)求EF的长
(2)证明:EF∥平面AA1D1D;
(3)证明:EF⊥平面A1CD.
 在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是D1D,BD的中点,G在棱CD上,且CG=
在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是D1D,BD的中点,G在棱CD上,且CG=| 1 | 4 |
(1)求证:EF⊥B1C;
(2)求EF与C1G所成的角的余弦;
(3)求FH的长.
 ,定义范数
,定义范数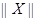 ,它满足以下性质:⑴
,它满足以下性质:⑴ ,当且仅当
,当且仅当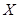 为零向量时,不等式取等号;⑵对任意的实数
为零向量时,不等式取等号;⑵对任意的实数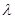 ,
, 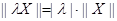 (注:此处点乘号为普通的乘号);⑶
(注:此处点乘号为普通的乘号);⑶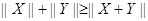 .应用类比的方法,我们可以给出空间直角坐标系下范数的定义,现有空间向量
.应用类比的方法,我们可以给出空间直角坐标系下范数的定义,现有空间向量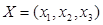 ,下面给出的几个表达式中,可能表示向量
,下面给出的几个表达式中,可能表示向量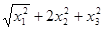 ⑵
⑵ 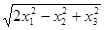 ⑶
⑶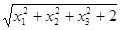 ⑷
⑷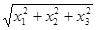
 -
-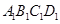 中,
中,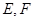 分别为
分别为 的中点. 应用空间向量方法求解下列问题.
的中点. 应用空间向量方法求解下列问题. 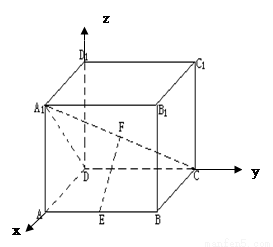
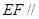 平面
平面 ;
;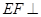 平面
平面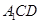 .
.