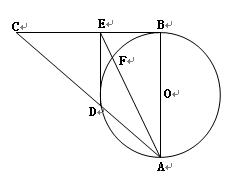
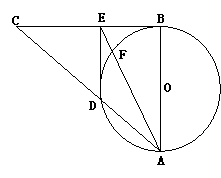
摘要:解:(1)过D作DE⊥BC.垂足为E.在Rt△BDC中,由∠BDC=90°,∠DCB=30°.BC=2.得BD=1.CD=.∴DE=CD·sin30°=. OE=OB-BE=OB-BD·cos60°=1-. ∴D点坐标为(0.-).即向量OD[TX→]的坐标为{0.-}. (2)依题意:. 所以. 设向量和的夹角为θ.则 cosθ= . 评述:本题考查空间向量坐标的概念.空间向量数量积的运算及空间向量的夹角公式.解决好本题的关键是对空间向量坐标的概念理解清楚.计算公式准确.同时还要具备很好的运算能力. ●命题趋向与应试策略 对本章内容的考查主要分以下三类:
网址:http://m.1010jiajiao.com/timu_id_4435247[举报]
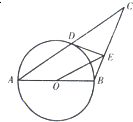 选修4-1:几何证明选讲
选修4-1:几何证明选讲如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连接OE.若CD=
| 3 |
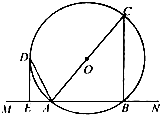 (2013•唐山一模)选修4-1:几何证明选讲
(2013•唐山一模)选修4-1:几何证明选讲 EA.
EA. 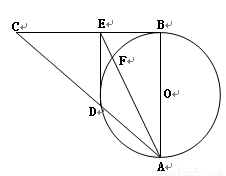
 EA.
EA.