摘要：(1)证明:∵PA⊥平面ABCD.∴PA⊥AB.又AB⊥AD.∴AB⊥平面PAD.又∵AE⊥PD.∴PD⊥平面ABE.故BE⊥PD. (2)解:以A为原点.AB.AD.AP所在直线为坐标轴.建立空间直角坐标系.则点C.D的坐标分别为(a.a.0).(0.2a.0). ∵PA⊥平面ABCD.∠PDA是PD与底面ABCD所成的角.∴∠PDA=30°. 于是.在Rt△AED中.由AD=2a.得AE=a.过E作EF⊥AD.垂足为F.在Rt△AFE中.由AE=a.∠EAF=60°.得AF=.EF=a.∴E(0.a) 于是.={-a.a.0} 设与的夹角为θ.则由cosθ= ∴θ=arccos.即AE与CD所成角的大小为arccos. 评述:第(2)小题中.以向量为工具.利用空间向量坐标及数量积.求两异面直线所成的角是立体几何中的常见问题和处理手段.
网址：http://m.1010jiajiao.com/timu_id_4435246[举报]
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1.
（Ⅰ）证明PC⊥AD；
（Ⅱ）求二面角A-PC-D的正弦值；
（Ⅲ）设E为棱PA上的点，满足异面直线BE与CD所成的角为30°，求AE的长.
【解析】解法一：如图，以点A为原点建立空间直角坐标系，依题意得A(0,0,0)，D(2,0,0),C(0,1,0),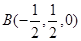 
,P（0,0,2）.
（1）证明：易得
，
于是
,所以
(2) ,
设平面PCD的法向量
，
则
,即
.不防设
，可得
.可取平面PAC的法向量
于是
从而
.
所以二面角A-PC-D的正弦值为
.
（3）设点E的坐标为（0,0，h），其中
，由此得
.
由，故
所以，
，解得
，即
.
解法二：（1）证明：由
，可得
，又由
,
,故
.又
,所以.
(2)如图，作
于点H，连接DH.由,
,可得
.
因此
,从而
为二面角A-PC-D的平面角.在
中，
,由此得
由（1）知
,故在
中，
因此
所以二面角
的正弦值为.
（3）如图，因为
，故过点B作CD的平行线必与线段AD相交，设交点为F，连接BE，EF. 故
或其补角为异面直线BE与CD所成的角.由于BF∥CD，故
.在
中，
故
在
中，由
,
,
可得
.由余弦定理，
,
所以.
查看习题详情和答案>>