摘要:(1)证明:∵=-2-2+4=0.∴AP⊥AB. 又∵=-4+4+0=0.∴AP⊥AD. ∵AB.AD是底面ABCD上的两条相交直线.∴AP⊥底面ABCD. (2)解:设与的夹角为θ.则 cosθ= V=||·||·sinθ·||= (3)解:|(×)·|=|-4-32-4-8|=48它是四棱锥P-ABCD体积的3倍. 猜测:|(×)·|在几何上可表示以AB.AD.AP为棱的平行六面体的体积(或以AB.AD.AP为棱的直四棱柱的体积). 评述:本题考查了空间向量的坐标表示.空间向量的数量积.空间向量垂直的充要条件.空间向量的夹角公式和直线与平面垂直的判定定理.棱锥的体积公式等.主要考查考生的运算能力.综合运用所学知识解决问题的能力及空间想象能力.
网址:http://m.1010jiajiao.com/timu_id_4435242[举报]
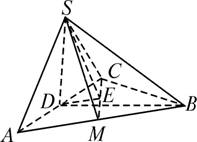
如图,在四棱锥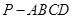 中,底面ABCD是一直角梯形,
中,底面ABCD是一直角梯形,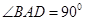 ,
, ,
,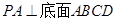 ,且PA=AD=DC=
,且PA=AD=DC= AB=1.
AB=1.
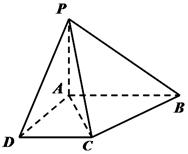
(1)证明:平面 平面
平面
(2)设AB,PA,BC的中点依次为M、N、T,求证:PB∥平面MNT
(3)求异面直线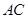 与
与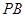 所成角的余弦值
所成角的余弦值
查看习题详情和答案>>
(本小题满分12分)
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足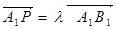
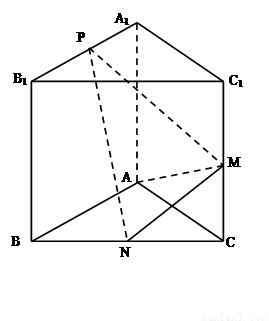
(1)证明:PN⊥AM
(2)若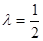 ,求直线AA1与平面PMN所成角的正弦值.
,求直线AA1与平面PMN所成角的正弦值.
查看习题详情和答案>>
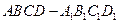 中,
中,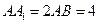 ,点
,点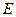 在
在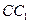
 上且
上且
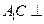 平面
平面 ;
;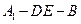 的余弦值.
的余弦值.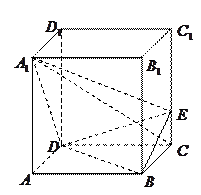
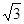 ,-1), B=(
,-1), B=(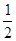 ,
,
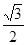 ),O为原点。
),O为原点。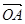 ,b=
,b=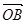 ,若存在不同时为零的实数k、t,使得x=a+(t2-3)b,y=-ka+tb,且x⊥y,求函数关系式k=f(t).
,若存在不同时为零的实数k、t,使得x=a+(t2-3)b,y=-ka+tb,且x⊥y,求函数关系式k=f(t).