摘要:应用函数思想解题.确立变量之间的函数关系是一关键步骤.大体可分为下面两个步骤:(1)根据题意建立变量之间的函数关系式.把问题转化为相应的函数问题,(2)根据需要构造函数.利用函数的相关知识解决问题,(3)方程思想:在某变化过程中.往往需要根据一些要求.确定某些变量的值.这时常常列出这些变量的方程或.通过解方程求出它们.这就是方程思想,
网址:http://m.1010jiajiao.com/timu_id_4433217[举报]
把函数 的图象按向量
的图象按向量 平移得到函数
平移得到函数 的图象.
的图象.
(1)求函数 的解析式; (2)若
的解析式; (2)若 ,证明:
,证明: .
.
【解析】本试题主要考查了函数 平抑变换和运用函数思想证明不等式。第一问中,利用设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 ,便可以得到结论。第二问中,令
,便可以得到结论。第二问中,令 ,然后求导,利用最小值大于零得到。
,然后求导,利用最小值大于零得到。
(1)解:设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 得y-2=ln(x+1)-2即y=ln(x+1),所以
得y-2=ln(x+1)-2即y=ln(x+1),所以 .……4分
.……4分
(2) 证明:令 ,……6分
,……6分
则 ……8分
……8分
 ,∴
,∴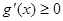 ,∴
,∴ 在
在 上单调递增.……10分
上单调递增.……10分
故 ,即
,即
查看习题详情和答案>>
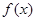 ,在使
,在使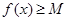 成立的所有常数M中,我们把M的最大值称为函数
成立的所有常数M中,我们把M的最大值称为函数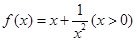 上的“下确界”为 .
上的“下确界”为 .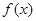 ,在使
,在使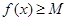 成立的所有常数
成立的所有常数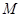 中,我们把
中,我们把 的"下确界"等于_________.
的"下确界"等于_________. 其中a>0.
其中a>0.