摘要:由已知得sinα==.tan==. 法二:tan===.
网址:http://m.1010jiajiao.com/timu_id_4429173[举报]
学生李明解以下问题已知α,β,?均为锐角,且sinα+sin?=sinβ,cosβ+cos?=cosα求α-β的值
其解法如下:由已知sinα-sinβ=-sin?,cosα-cosβ=cos?,两式平方相加得2-2cos(α-β)=1
∴cos(α-β)=
又α,β均锐角
∴-
<α-β<
∴α-β=±
请判断上述解答是否正确?若不正确请予以指正.
查看习题详情和答案>>
其解法如下:由已知sinα-sinβ=-sin?,cosα-cosβ=cos?,两式平方相加得2-2cos(α-β)=1
∴cos(α-β)=
| 1 |
| 2 |
∴-
| π |
| 2 |
| π |
| 2 |
∴α-β=±
| π |
| 3 |
请判断上述解答是否正确?若不正确请予以指正.
学生李明解以下问题已知α,β,?均为锐角,且sinα+sin?=sinβ,cosβ+cos?=cosα求α-β的值
其解法如下:由已知sinα-sinβ=-sin?,cosα-cosβ=cos?,两式平方相加得2-2cos(α-β)=1
∴cos(α-β)=
又α,β均锐角
∴-
<α-β<
∴α-β=±
请判断上述解答是否正确?若不正确请予以指正.
查看习题详情和答案>>
其解法如下:由已知sinα-sinβ=-sin?,cosα-cosβ=cos?,两式平方相加得2-2cos(α-β)=1
∴cos(α-β)=
| 1 |
| 2 |
∴-
| π |
| 2 |
| π |
| 2 |
∴α-β=±
| π |
| 3 |
请判断上述解答是否正确?若不正确请予以指正.
已知函数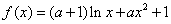 .
.
(Ⅰ)讨论函数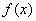 的单调性;
的单调性;
(Ⅱ)设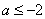 ,证明:对任意
,证明:对任意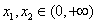 ,
,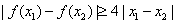 .
.
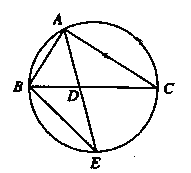 1.选修4-1:几何证明选讲
1.选修4-1:几何证明选讲
如图, 的角平分线
的角平分线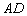 的延长线交它的外接圆于点
的延长线交它的外接圆于点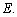
(Ⅰ)证明: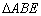 ∽△
∽△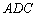 ;
;
(Ⅱ)若 的面积
的面积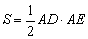 ,求
,求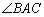 的大小.
的大小.
证明:(Ⅰ)由已知条件,可得∠BAE=∠CAD.
因为∠AEB与∠ACB是同弧上的圆周角,所以∠AEB=∠ACD.
故△ABE∽△ADC.
(Ⅱ)因为△ABE∽△ADC,所以 ,即AB·AC=AD·AE.
,即AB·AC=AD·AE.
又S= AB·ACsin∠BAC,且S=
AB·ACsin∠BAC,且S= AD·AE,故AB·ACsin∠BAC=AD·AE.
AD·AE,故AB·ACsin∠BAC=AD·AE.
则sin∠BAC=1,又∠BAC为三角形内角,所以∠BAC=90°.
查看习题详情和答案>>
 ,给出下列命题:①
,给出下列命题:①  的图象可以看作是由y=sin2x的图象向左平移
的图象可以看作是由y=sin2x的图象向左平移 个单位而得;②
个单位而得;②  而得;③ 函数y=|
而得;③ 函数y=| ;④
函数y=|
;④
函数y=|