摘要：设三角形的三顶点是A(x1,y1).B(x2,y2).C(x3,y3),则⊿ABC的重心G为(),
网址：http://m.1010jiajiao.com/timu_id_4428735[举报]
以正方形ABCD的相对顶点A、C为焦点的椭圆，恰好过正方形四边的中点，则该椭圆的离心率为
；设F1和F2为双曲线
-
=1（a＞0，b＞0）的两个焦点，若F1，F2，P（0，2b）是正三角形的三个顶点，则双曲线的离心率为
x2的焦点作直线交抛物线于A（x1，y1），B（x2，y2）两点，若y1+y2=5，则线段AB的长等于
查看习题详情和答案>>
| ||||
| 2 |
| ||||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
2
2
；经过抛物线y=| 1 |
| 4 |
7
7
．
已知点G是△ABC的重心，A（0，-1），B（0，1）.在x轴上有一点M，满足|
|=|
|，
=λ
(λ∈R)（若△ABC的顶点坐标为?A(x1,y1),B(x2,y2),C(x3,y3)，则该三角形的重心坐标为G(
,
)).
|=||，=λ(λ∈R)（若△ABC的顶点坐标为?A(x1,y1),B(x2,y2),C(x3,y3)，则该三角形的重心坐标为G(,)).（1）求点C的轨迹E的方程；
（2）设（1）中曲线E的左、右焦点分别为F1、F2，过点F2的直线l交曲线E于P、Q两点，求△F1PQ面积的最大值，并求出取最大值时直线l的方程.
查看习题详情和答案>>
已知点G是△ABC的重心，A（0，-1），B（0，1）．在x轴上有一点M，满足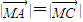
，
（若△ABC的顶点坐标为A（x1，y1），B（x2，y2），C（x3，y3），则该三角形的重心坐标为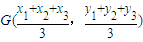
）．
（1）求点C的轨迹E的方程．
（2）设（1）中曲线E的左、右焦点分别为F1、F2，过点F2的直线l交曲线E于P、Q两点，求△F1PQ面积的最大值，并求出取最大值时直线l的方程．
查看习题详情和答案>>
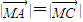，（若△ABC的顶点坐标为A（x1，y1），B（x2，y2），C（x3，y3），则该三角形的重心坐标为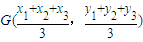）．（1）求点C的轨迹E的方程．
（2）设（1）中曲线E的左、右焦点分别为F1、F2，过点F2的直线l交曲线E于P、Q两点，求△F1PQ面积的最大值，并求出取最大值时直线l的方程．
查看习题详情和答案>>
，
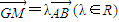（若△ABC的顶点坐标为A（x1，y1），B（x2，y2），C（x3，y3），则该三角形的重心坐标为
）．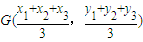